
(本题10分)已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
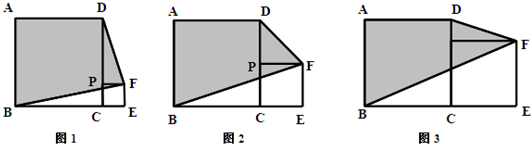
1.观察计算:(1)如图1,当a=4,b=1时,四边形ABFD的面积为 ;
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 ;
2.探索发现:(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论;

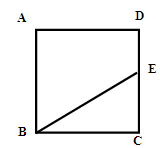
3.综合应用:(5)农民赵大伯有一块正方形的土地(如图),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.(要求尺规作图,保留作图痕迹)
1.(1)4×4+(1+4)×1÷2-1×5÷2=16;2)4×4+(2+4)×2÷2-2×6÷2=16;
(3)4×4+(3+4)×3÷2-3×7÷2=16
2.(4)无论点P在CD边上的什么位置,四边形ABFD的面积与正方形ABCD的面积相等,与正方形PCEF的边长无关.
证明:连接BD,CF,∵四边形ABCD是正方形,∴∠DBC=45°,
同理∠FCE=45°,∴BD∥CF,∴S△BCD=S△BDF,
∴四边形ABFD的面积与正方形ABCD的面积相等;

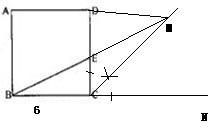
3.(5)如图6,作BC的延长线CN,作∠DCN的角平分线交BE的延长线于点M,则四边形ABMD的面积与正方形ABCD的面积相等,点M即为所求.
解析:略


科目:初中数学 来源: 题型:
(本题10分)已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数的图象与y轴相交于点Q(0,4)
1.(1)求这两个函数的解析式
2.(2)在同一坐标系内,分别画出这两个函数的图象
3.(3)求出![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题10分)已知,如图,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,抛物线
,抛物线![]() 上的两点
上的两点![]() 的横坐标分别为
的横坐标分别为![]() 1和4,直线
1和4,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 分别作直线
分别作直线![]() 的垂线,垂足分别为点
的垂线,垂足分别为点![]() 、
、![]() ,连接
,连接![]() .
.
1.(1)求点![]() 的坐标;
的坐标;
2.(2)求证:![]() ;
;
3.(3)点![]() 是抛物线
是抛物线![]() 对称轴右侧图象上的一动点,过点
对称轴右侧图象上的一动点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,是否存在点
,是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省南通市幸福中学八年级上学期期中考试数学卷 题型:解答题
(本题10分)已知:如图所示,
【小题1】(1)作出△ABC关于y轴对称的△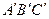 ,并写出△
,并写出△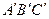 三个顶点的坐标.
三个顶点的坐标.
【小题2】(2) 在x轴上画出点P,使PA+PC最小.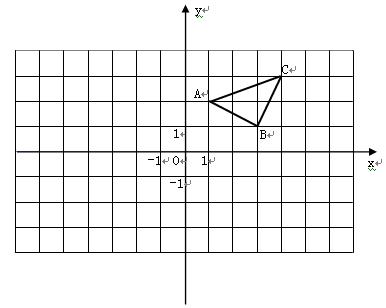
查看答案和解析>>
科目:初中数学 来源:2012届江苏省苏州市高新区九年级上学期期末考试数学卷 题型:解答题
(本题10分)已知:直角梯形OABC中,BC//OA,∠AO C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛
C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛 物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.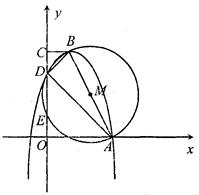
【小题1】(1)写出顶点B的坐标 ▲ (用a的代数式表示);
【小题2】(2)求抛物线的解析式:
【小题3】(3)在x轴下方的抛物线上是否存在这样的点P:过点P作PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省苏州市高新区九年级上学期期末考试数学卷 题型:解答题
(本题10分)已知:直角梯形OABC中,BC//OA,∠AOC=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
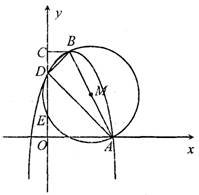
1.(1)写出顶点B的坐标 ▲ (用a的代数式表示);
2.(2)求抛物线的解析式:
3.(3)在x轴下方的抛物线上是否存在这样的点P:过点P作PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标:若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com