
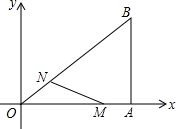
 如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:分析 (1)由勾股定理求出OB,作NP⊥OA于P,则NP∥AB,得出△OPN∽△OAB,得出比例式$\frac{PN}{AB}=\frac{OP}{OA}=\frac{ON}{OB}$,求出OP、PN,即可得出点N的坐标;
(2)由三角形的面积公式得出S是x的二次函数,即可得出S的最大值;
(3)分两种情况:①若∠OMN=90°,则MN∥AB,由平行线得出△OMN∽△OAB,得出比例式,即可求出x的值;
②若∠ONM=90°,则∠ONM=∠OAB,证出△OMN∽△OBA,得出比例式,求出x的值即可.
解答 解:(1)根据题意得:MA=x,ON=1.25x,
在Rt△OAB中,由勾股定理得:OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
作NP⊥OA于P,如图1所示:
则NP∥AB,
∴△OPN∽△OAB,
∴$\frac{PN}{AB}=\frac{OP}{OA}=\frac{ON}{OB}$,
即$\frac{PN}{3}=\frac{OP}{4}=\frac{1.25x}{5}$,
解得:OP=x,PN=$\frac{3}{4}x$,
∴点N的坐标是(x,$\frac{3}{4}x$);
(2)在△OMN中,OM=4-x,OM边上的高PN=$\frac{3}{4}x$,
∴S=$\frac{1}{2}$OM•PN=$\frac{1}{2}$(4-x)•$\frac{3}{4}x$=-$\frac{3}{8}$x2+$\frac{3}{2}$x,
∴S与x之间的函数表达式为S=-$\frac{3}{8}$x2+$\frac{3}{2}$x(0<x<4),
配方得:S=-$\frac{3}{8}$(x-2)2+$\frac{3}{2}$,
∵-$\frac{3}{8}$<0,
∴S有最大值,
当x=2时,S有最大值,最大值是$\frac{3}{2}$;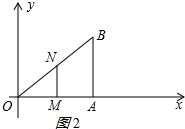
(3)存在某一时刻,使△OMN是直角三角形,理由如下:
分两种情况:①若∠OMN=90°,如图2所示:
则MN∥AB,
此时OM=4-x,ON=1.25x,
∵MN∥AB,
∴△OMN∽△OAB,
∴$\frac{OM}{OA}=\frac{ON}{OB}$,
即$\frac{4-x}{4}=\frac{1.25x}{5}$,
解得:x=2;
②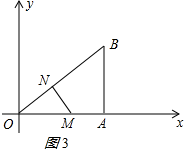 若∠ONM=90°,如图3所示:
若∠ONM=90°,如图3所示:
则∠ONM=∠OAB,
此时OM=4-x,ON=1.25x,
∵∠ONM=∠OAB,∠MON=∠BOA,
∴△OMN∽△OBA,
∴$\frac{OM}{OB}=\frac{ON}{OA}$,
即$\frac{4-x}{5}=\frac{1.25x}{4}$,
解得:x=$\frac{64}{41}$;
综上所述:x的值是2秒或$\frac{64}{41}$秒.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、勾股定理、坐标与图形特征、直角三角形的性质、三角形面积的计算、求二次函数的解析式以及最值等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,通过证明三角形相似才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤2 | B. | x≤2且x≠1 | C. | x<2且x≠1 | D. | x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
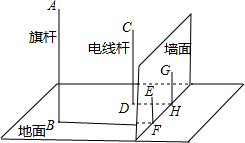 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
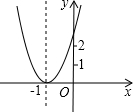 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com