
分析 (1)原式各项化为最简二次根式,合并即可得到结果;
(2)原式利用零指数幂、负整数指数幂法则,算术平方根以及绝对值的代数意义化简,计算即可得到结果;
(3)方程组利用加减消元法求出解即可.
解答 解:(1)原式=4$\sqrt{2}$-4$\sqrt{3}$-3$\sqrt{3}$+2$\sqrt{2}$=6$\sqrt{2}$-7$\sqrt{3}$;
(2)原式=$\frac{1}{9}$+4-1+$\frac{8}{9}$=4;
(3)$\left\{\begin{array}{l}{3x-y=7①}\\{5x+2y=8②}\end{array}\right.$,
①×2+②得:11x=22,即x=2,
把x=2代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
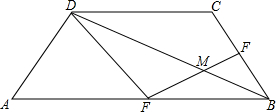 如图,梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
如图,梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
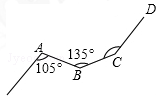 如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角A是105°,第二才拐的角B是135°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C的度数为( )
如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角A是105°,第二才拐的角B是135°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C的度数为( )| A. | 130° | B. | 135° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
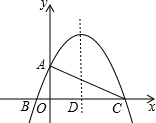 如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com