
【题目】如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.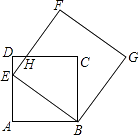
(1)当E为边AD的中点时,求DH的长;
(2)当tan∠ABE= ![]() 时,连接CF,求CF的长;
时,连接CF,求CF的长;
(3)连接CE,求△CEF面积的最小值.
【答案】
(1)
解:∵四边形ABCD和四边形BGFE是正方形,
∴∠D=∠A=∠BEF=90°,
∴∠AEB+∠DEH=∠DEH+∠DHE=90°,
∴∠AEB=∠DHE,
∴△EDH∽△BAE,
∴ ![]() ,
,
∵E为边AD的中点,
∴DE=AE=8,
∴ ![]() ,
,
∴DH=4;
(2)
解:过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,
∵tan∠ABE= ![]() ,AB=16,
,AB=16,
∴AE=12,
∴DE=4,
∵∠MEF+∠AEB=∠AEB+∠ABE=90°,
∴∠MEF=∠ABE,
∴tan∠MEF= ![]() ,
,
∴ME=16,FM=12,
∴DM=12,
∴DM=MF,
∴四边形DGFM是正方形,
∴FG=12,HG=9,
∴CG=4,
∴FC= ![]() =4
=4 ![]()
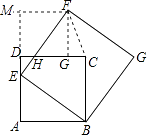
(3)
解:∵S△CEF=S△CHF+S△CHE= ![]() CHEM,
CHEM,
∵△EMF≌△BAE,
∴EM=AB=16,
∴S△CEF=8CH,
∵△EDH∽△BAE,
∴ ![]() ,
,
设AE为x,则DH= ![]() (﹣x2+16x)=﹣
(﹣x2+16x)=﹣ ![]() (x﹣8)2+4≤4,
(x﹣8)2+4≤4,
∴DH≤4,
∴CH≥12,CH最小值是12,
∴△CEF面积的最小值是96
【解析】(1)根据正方形的性质得到∠D=∠A=∠BEF=90°,根据余角的性质得到∠AEB=∠DHE,根据相似三角形的想知道的 ![]() ,代入数据即可得到结论;(2)过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,根据已知条件得到AE=12,求得DE=4,根据余角的性质得到∠MEF=∠ABE,等量代换得到tan∠MEF=
,代入数据即可得到结论;(2)过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,根据已知条件得到AE=12,求得DE=4,根据余角的性质得到∠MEF=∠ABE,等量代换得到tan∠MEF= ![]() 求得ME=16,FM=12,根据勾股定理即可得到结论;(3)由于S△CEF=S△CHF+S△CHE=
求得ME=16,FM=12,根据勾股定理即可得到结论;(3)由于S△CEF=S△CHF+S△CHE= ![]() CHEM,根据全等三角形的性质得到EM=AB=16,求得S△CEF=8CH,根据相似三角形的性质得到
CHEM,根据全等三角形的性质得到EM=AB=16,求得S△CEF=8CH,根据相似三角形的性质得到 ![]() ,设AE为x,于是得到DH=
,设AE为x,于是得到DH= ![]() (﹣x2+16x)=﹣
(﹣x2+16x)=﹣ ![]() (x﹣8)2+4≤4,即可得到结论.
(x﹣8)2+4≤4,即可得到结论.
【考点精析】本题主要考查了正方形的性质和相似三角形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图1,在矩形纸片ABCD和矩形纸片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,点E是AD的中点,矩形纸片EFGH以点E为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图1,当EF与AB相交于点M,EH与BC相交于点N时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当AM=CN时,AM与BM有怎样的数量关系,说明理由.
(3)“创新”小组提出的问题是;若矩形EFGH继续以点E为旋转中心进行逆时针旋转,当∠AEF=60°时,请你在图2中画出旋转后的示意图,并求出此时EF将边BC分成的两条线段的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果10b=n,那么称b为n的劳格数,记为b= d(n).
(1)根据劳格数的定义,可知d(10)=1,d(102)=2,直接写出 d(103)的值.
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)= d(m)+ d(n);d(![]() )= d(m)- d(n).
)= d(m)- d(n).
根据运算性质,求:![]() ,若
,若 ![]() ,直接写出
,直接写出![]() ,
,![]() 的值.
的值.
(3)下表中与数x对应的劳格数 ![]() 有且只有两个是错误的,请找出错误的劳格数并改正.
有且只有两个是错误的,请找出错误的劳格数并改正.
| 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一条12个单位长度的线段分成三条线段,其中一条线段成为4个单位长度,另两条线段长都是单位长度的整数倍.![]()
(1)不同分段得到的三条线段能组成多少个不全等的三角形?用直尺和圆规作这些三角形(用给定的单位长度,不写作法,保留作图痕迹);
(2)求出(1)中所作三角形外接圆的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F. 
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA= ![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教师运动会中,甲,乙两组教师参加“两人背夹球”往返跑比赛,即:每组两名教师用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.若距起点的距离用y(米)表示,时间用x(秒)表示.下图表示两组教师比赛过程中y与x的函数关系的图象.根据图象,有以下四个推断:
①乙组教师获胜
②乙组教师往返用时相差2秒
③甲组教师去时速度为0.5米/秒
④返回时甲组教师与乙组教师的速度比是2:3
其中合理的是( )
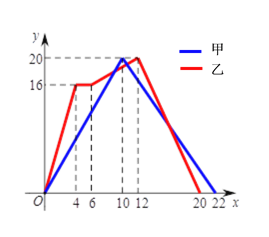
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com