
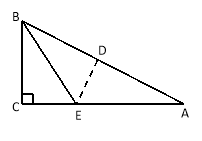
【题目】在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,如图,使点A和点B重合,折痕与AB、AC分别相交于点D和点E,折痕DE的长为
【答案】1
【解析】先根据,∠C=90°,∠A=30°,AC=3求出AB的长,再根据图形翻折变换的性质可知DE⊥AB,AE=BE=![]() AB,再在Rt△ADE中,由DE=AEtan∠A即可得出DE的长.
AB,再在Rt△ADE中,由DE=AEtan∠A即可得出DE的长.
解:∵△ABC中,∠C=90°,∠A=30°,AC=3,
∴AB=![]() =
=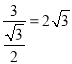 ,
,
∵△BDE是△ADE翻折而成,DE为折痕,
∴DE⊥AB,AE=BE=![]() AB=
AB=![]() ×2
×2![]() =
=![]() ,
,
在Rt△ADE中,DE=AEtan∠A=![]() ×tan30°=
×tan30°=![]() ×
×![]() =1.
=1.
故答案为:1.
考查的是图形翻折变换的性质及三角函数的定义,熟知“折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等”是解答此题的关键


科目:初中数学 来源: 题型:
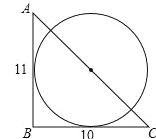
【题目】如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是 .
①圆心O是∠B的角平分线与AC的交点;
②圆心O是∠B的角平分线与AB的垂直平分线的交点;
③圆心O是AB的垂直平分线与BC的垂直平分线的交点;
④圆心O是∠B的角平分线与BC的垂直平分线的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①棱柱的侧面是长方形;②棱柱的侧面可能是三角形;③正方体的所有棱长都相等;④棱柱的所有侧棱长都相等.其中正确的有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
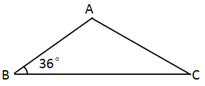
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的“三阶等腰线”.
(1)请你在图1,图2中用两种不同的方法画出顶角为36°的等腰三角形的“三阶等腰线”,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种).
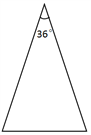



图1 图2 备用1 备用2
(2)△ABC中,∠B=36°,AD和DE是△ABC的“三阶等腰线”,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
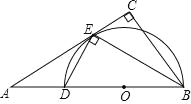
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=2![]() ,AE=6,求EC的长.
,AE=6,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校随机抽查的20名八年级男生的身高统计表:
身高(cm) | 150 | 155 | 160 | 163 | 165 | 168 |
人数(人) | 1 | 3 | 4 | 4 | 5 | 3 |
这组数据的众数是__cm,中位数是__cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com