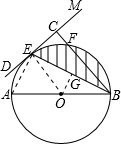
解:(1)连接AE.
∵AB是⊙O的直径,
∴∠AEB=90°,
又∵BC⊥DM,
∴∠ECB=90°,
∴∠AEB=∠ECB,
∵直线DM与⊙O相切于点E,
∴∠CEB=∠EAB,
∴△AEB∽△ECB,
∴
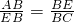
,
∴BE
2=AB•BC,
∴BE=

(cm);
(2)连接OE,过点O作OG⊥BE于点G.
∴BG=EG,
在Rt△ABE中,cos∠ABE=
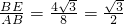
,
∴∠ABE=30°,
在Rt△OBG中,∠ABE=30°,BO=4,
∴OG=2,
∴
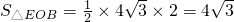
,
∵OE=OB,
∴∠OEB=∠OBE=30°,
∴∠BOE=120°,
∴S
扇形OBE=
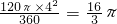
,
∴S
阴影=S
扇形OBE-S
△EOB=(
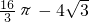
)cm
2.
分析:(1)连接AE,易得∠AEB=90°,∠ECB=90°,那么∠AEB=∠ECB,根据弦切角定理得∠CEB=∠EAB,那么△AEB∽△ECB,由相似三角形的性质得BE
2=AB•BC,从而求得BE的值;
(2)连接OE,过点O作OG⊥BE于点G,易得BG=EG,根据特殊角的三角函数值知∠ABE=30°,所以可求得BO=4,OG=2,进而求得△EOB的面积,由于半径OE=OB,根据等边对等角得∠OEB=∠OBE=30°,由三角形的内角和定理得∠BOE=120°,则可求得扇形OBE的面积,再根据S
阴影=S
扇形OBE-S
△EOB求得阴影部分的面积.
点评:本题综合考查了直径对的圆周角是直角三角形,弦切角定理,切线的性质,相似三角形的判定和性质,垂径定理,锐角三角函数的概念,特殊角的三角函数值,三角形和扇形的面积公式等知识点.

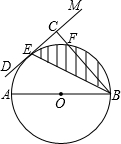 点F,BC=6cm.
点F,BC=6cm. 解:(1)连接AE.
解:(1)连接AE.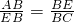 ,
, (cm);
(cm);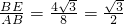 ,
,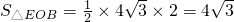 ,
,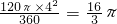 ,
,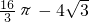 )cm2.
)cm2.

 阅读快车系列答案
阅读快车系列答案