
【题目】某商店出售A、B两种商品,一月份这两种商品的利润都是10万元,后因某种原因确定增加出售A种商品的数量,使A种商品每月利润的增长率都为a,同时减少B种商品的数量,使B种商品每月利润减少的百分率也都是a,(1)分别求出二月份出售A和B两种商品的利润是多少万元?(2)求出三月份出售A、B两种商品的总利润是多少万元?
【答案】(1)A种设备每台的成本是4万元,B种设备每台的成本是6万元.(2)该公司一共获利114万元.
【解析】
(1)设A种设备每台的成本是x万元,B种设备每台的成本是1.5x万元.根据数量=总价÷单价结合“投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台”,即可得出关于x的分式方程,解之经检验后即可得出结论.
(2)根据“利润=售价-成本”分别列式计算出A,B种设备的利润为4.8万元,9万元,即可计算出该公司获得的总利润.
(1)设A种设备每台的成本是x万元,则B种设备每台的成本是1.5x万元。
根据题意得:![]()
解得:x=4
经检验x=4是分式方程的解
∴1.5x=6.
答:A种设备每台的成本是4万元,B种设备每台的成本是6万元.
(2)优惠后A种的售价为:6×0.8=4.8(万元)
优惠后B种的售价为:10×(1-10%)=9(万元)
(4.84)×30+(96)×30=114(万元)
答:设备全部售出,该公司一共获利114万元.


科目:初中数学 来源: 题型:
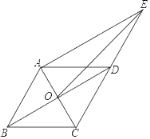
【题目】已知菱形ABCD,对角线交点为O,延长CD至E且CD=DE.下列判断正确个数是( )
(1)∠AOB=90°;(2)AE=2OD;(3)∠OAE=90°;(4)∠AEO=∠CEO.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=![]() x与双曲线
x与双曲线![]() 交于A、B两点,且点A的坐标为(6,m).
交于A、B两点,且点A的坐标为(6,m).
(1)求双曲线![]() 的解析式;
的解析式;
(2)点C(n,4)在双曲线![]() 上,求△AOC的面积;
上,求△AOC的面积;
(3)在(2)的条件下,在x轴上找出一点P,使△AOC的面积等于△AOP的面积的三倍.请直接写出所有符合条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100;
九(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | p | 8.4 |
(1)直接写出表中m、n、p的值为:m=______,n=______,p=______;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好.”但也有人说(2)班的成绩要好.请给出两条支持九(2)班成绩更好的理由;
(3)学校确定了一个标准成绩,等于或大于这个成绩的学生被评定为“优秀”等级,如果九(2)班有一半的学生能够达到“优秀”等级,你认为标准成绩应定为______分,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
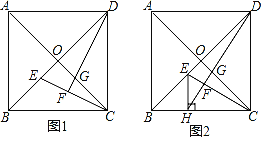
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,P为直线AD上一点,以PD为边做正方形PDEF,使点E在线段CD的延长线上,连接AC、AF.若![]() ,则
,则![]() 的度数为________.
的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有450名学生,随机抽取其中的若干名学生,根据这些学生两次数学模拟考试成绩,分别绘制了如下所示的频数分布直方图,其中图②不完整.
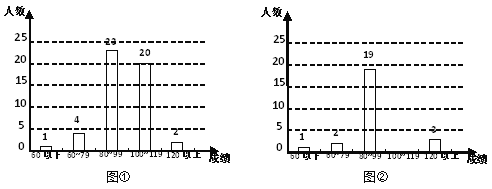
注:① 成绩均为整数;②“60以下”不含60,其余分数段均包含端点;③ 图①、图②分别表示第一次、第二次模拟考试成绩频数分布直方图.
根据以上信息,解答下列问题:
(1)把图②补全;
(2)规定100分以上为优秀,请计算图②中达到优秀的比例;
(3)请你估算九年级学生第二次数学模拟考试达到优秀的人数比第一次数学模拟考试增加多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下文,回答问题:
已知:(1-x)(1+x)=1-x2.
(1-x)(1+x+x2)=_______;
(1-x)(1+x+x2+x3)=_______;
(1)计算上式并填空;
(2)猜想:(1-x)(1+x+x2+…+xn)= ;
(3)你能计算399+398+397…+32+3+1的结果吗?请写出计算过程(结果用含有3幂的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com