
分析 (1)设一次函数的解析式为y=kx+b,由已知一次函数的图象与直线y=3x+3平行,推出k=3,因为经过点(1,2),推出b=-1.
(2)如图,直线y=3x+3与y轴的交点为P(-1,0),通过计算发现点P满足条件,再根据对称性求出P′点坐标即可.
解答 解:(1)设一次函数的解析式为y=kx+b,
∵已知一次函数的图象与直线y=3x+3平行,
∴k=3,
∵经过点(1,2),
∴2=3+b,
∴b=-1,
∴一次函数的解析式为y=3x-1.
(2)如图,直线y=3x+3与y轴的交点为P(-1,0),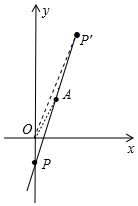
∵S△PAO=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
∴点P(0,-1)满足条件,
∴P关于点A的对称点P′(2,5),
∵PA=P′A,
∴S△P′OA=S△POA=$\frac{1}{2}$,
∴满足条件的点P坐标为(-1,0)或(2,5).
点评 本题考查一次函数、两直线平行的条件,三角形的面积等知识,解题的关键是寻找特殊点解决问题,属于中考常考题型.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
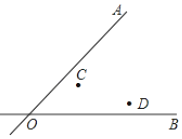 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要在∠AOB内部修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要在∠AOB内部修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.7724×104元 | B. | 7.724×103元 | C. | 7.724×1011元 | D. | 0.7724×1012元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
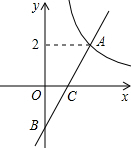 已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).
已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
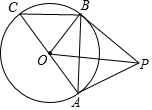 如图,已知AC是⊙O的直径,BC是⊙O的弦,P是⊙O外一点,连接PB,AB,OB,且∠PBA=∠ACB.
如图,已知AC是⊙O的直径,BC是⊙O的弦,P是⊙O外一点,连接PB,AB,OB,且∠PBA=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于A、B、C,直线DF分别交l1、l2、l3于D、E、F,AC交DF于H,若AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为$\frac{3}{5}$,$\frac{DH}{HF}$的值为$\frac{1}{3}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于A、B、C,直线DF分别交l1、l2、l3于D、E、F,AC交DF于H,若AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为$\frac{3}{5}$,$\frac{DH}{HF}$的值为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com