
分析 利用由已知条件方程x2-4x+d=0有实数根,可得出一元二次方程根的判别式,△=b2-4ac≥0,求出d的取值范围,结合圆的半径是4,得出d与r大小关系,当d=r,点P在⊙O上;当d<r,点P在⊙O的内部,根据点与圆的位置关系得出p与圆的位置关系.
解答 解:∵方程x2-4x+d=0有实数根,
∴△=b2-4ac=16-4d≥0,
∴d≤4,
∴d≤r;
当d<r,
∴点P在⊙O的内部,
当d=r,
∴点P在⊙O上;
∴点P在⊙O的内部或点P在⊙O上.
故答案为:内或上.
点评 此题主要考查了一元二次方程根的判别式,以及点与圆的位置关系的判定,解决问题的关键是方程有实数根,即△=b2-4ac≥0.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
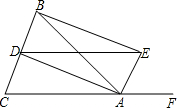 如图,在△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAF的平分线,BE⊥AE
如图,在△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAF的平分线,BE⊥AE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
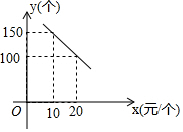 某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.
某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com