练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．（1）计算：$\sqrt{3}$（$\sqrt{2}$+$\sqrt{3}$）-$\sqrt{24}$
    （2）解方程：x2-2x=4．

    分析 （1）先算乘法，再合并即可；
    （2）先配方，再开方，即可求出答案．

    解答 解：（1）原式=$\sqrt{6}$+3-2$\sqrt{6}$
    =-$\sqrt{6}$+3；

    （2）x2-2x=4，
    x2-2x+1=4+1，
    （x-1）2=5，
    x-1=$±\sqrt{5}$，
    x1=1+$\sqrt{5}$，x2=1-$\sqrt{5}$．

    点评 本题考查了二次根式的混合运算，也考查了解一元二次方程，培养了学生的计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．如图，在4×4正方形网格中，黑色部分的 图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（　　）
    A．$\frac{3}{13}$B．$\frac{4}{13}$C．$\frac{5}{13}$D．$\frac{6}{13}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

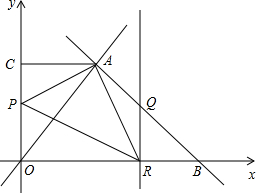    7．如图，已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A，且与x轴交于点B，过点A作AC⊥y轴与点C．点P从O点以每秒1个单位的速度沿折线O-C-A运动到A；点R从B点以相同的速度向O点运动，一个点到终点时，另一个点也随之停止运动．
    （1）求点A和点B的坐标；
    （2）过点R作直线l∥y轴，直线l交线段BA于点Q，设动点P运动的时间为t秒．
    ①当t为何值时，以A，P，O，R为顶点的四边形的面积为13？
    ②是否存在以A、P、R为顶点的三角形是等腰三角形？若存在，直接写出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，△ABC是直角三角形，∠ACB=90°，∠B=30°，以点C为旋转中心，将△ABC旋转到△A′B′C′的位置，且使A′B′经过点A．
    （1）求∠ACA′的度数，判断△ACA′的形状；
    （2）求线段AC与线段AB的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在△ABC中，AB=13，BC=10，BC边上的中线AD=12．
    （1）求证：AD⊥BC；
    （2）求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

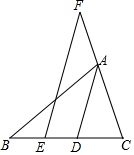    1．如图，在△ABC中，∠B=40°，∠C=70°，AD是△ABC的角平分线，点E在BD上，点F在CA的延长线上，EF∥AD．
    （1）求∠BAF的度数．
    （2）求∠F的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

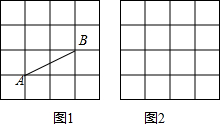    8．如图1，图2，正方形网格中每个小正方形的边长都是1，每个小正方形的顶点叫做格点．图1中的线段AB的两个端点都在格点上．
    （1）在图1中，线段AB的长为$\sqrt{5}$
    （2）在图1中，画一个等腰直角三角形ABC，且三角形的顶点都在格点上；
    （3）在图2中，画一个面积为10的正方形，且正方形的顶点都在格点上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．一元二次方程x2-2$\sqrt{2}$x+m=0有一个实数根是$\sqrt{2}$+$\sqrt{3}$，则m的值为-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知：如图，在?ABCD中，E、F是对角线BD上的两点，BE=DF，求证：AE=CF．

    查看答案和解析>>

    同步练习册答案