
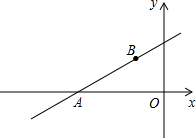
 ��ͼ��ֱ��l��y=$\frac{{\sqrt{3}}}{3}$x+m��x�ύ��A�㣬�Ҿ�����B��-$\sqrt{3}$��2������֪������C��y=ax2+bx+9��x��ֻ��һ�������㣬ǡΪA�㣮
��ͼ��ֱ��l��y=$\frac{{\sqrt{3}}}{3}$x+m��x�ύ��A�㣬�Ҿ�����B��-$\sqrt{3}$��2������֪������C��y=ax2+bx+9��x��ֻ��һ�������㣬ǡΪA�㣮���� ��1����B���������ֱ��l�Ľ���ʽ�������m��ֵ�����ֱ��l�Ľ���ʽ����ֱ��l��y�ύ�ڵ�C�����C�����������������Ǻ������������BAO�Ķ�����
��2��������ֵ�������߱ض�����0��9������������x��ֻ��һ��������A����A���������ߵĶ��㣬���Կ����������ߵĶ���ʽy=a��x+3$\sqrt{3}$��2������0��9�����붥��ʽ�������a��ֵ��
��3����P������Ϊ��h��0����������֪����P������A����࣬���Ե�P��A���Ҳ࣬���ڵ�P��D����AB�Գƣ��ҵ�D��������������C1�ϣ��������D���������������C1�Ľ���ʽ�������h��ֵ��
��� �⣺��1����B��-$\sqrt{3}$��2������y=$\frac{{\sqrt{3}}}{3}$x+m��
��2=-1+m��
��m=3��
��ֱ��l�Ľ���ʽΪy=$\frac{{\sqrt{3}}}{3}$x+3��
��ֱ��l��y�ύ�ڵ�C
��x=0����y=$\frac{{\sqrt{3}}}{3}$x+3��
��y=3��
��C��������0��3����
��y=0����y=$\frac{{\sqrt{3}}}{3}$x+3��
��x=-3$\sqrt{3}$��
��A��������-3$\sqrt{3}$��0����
��OC=3��OA=3$\sqrt{3}$��
��tan��BAO=$\frac{OC}{OA}=\frac{\sqrt{3}}{3}$��
���BAO=30�㣻
��2����x=0����y=ax2+bx+9��
��y=9
��������C������0��9����
�֡�������C��x��ֻ��һ�������㣬ǡΪA�㣬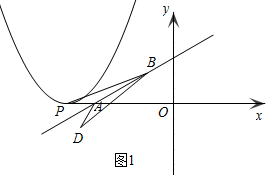
��A����������C�Ķ��㣬
�������ߵĶ���ʽΪy=a��x+3$\sqrt{3}$��2��
�ѣ�0��9������y=a��x+3$\sqrt{3}$��2��
��a=$\frac{1}{3}$��
��������C�Ľ���ʽΪy=$\frac{1}{3}$��x+3$\sqrt{3}$��2��
��3����������C1�Ľ���ʽΪy=$\frac{1}{3}$��x-h��2��
����P��A�����ʱ��
��Dһ������������C1�ϣ�
��������������⣬
����P��A���Ҳ�ʱ��
��ʱ��P��h��0��
��AP=h+3$\sqrt{3}$��
�ɶԳ��Կ�֪��AD=AP=h+3$\sqrt{3}$��
��DAB=��PAB=30�㣬
����D��DE��x���ڵ�E��
��AE=$\frac{1}{2}$AD=$\frac{h+3\sqrt{3}}{2}$��
DE=$\sqrt{3}$AE=$\frac{\sqrt{3}+9}{2}$��
��D��������$\frac{h-3\sqrt{3}}{2}$��$\frac{\sqrt{3}h+9}{2}$����
��D��$\frac{h-3\sqrt{3}}{2}$��$\frac{\sqrt{3}h+9}{2}$������y=$\frac{1}{3}$��x-h��2��
��$\frac{\sqrt{3}h+9}{2}$=$\frac{1}{3}$��$\frac{h+3\sqrt{3}}{4}$��2��
��h=21$\sqrt{3}$��h=-3$\sqrt{3}$��
��h=-3$\sqrt{3}$ʱ����ʱP��A�غϣ�
������������⣬
����������P��������21$\sqrt{3}$��0����
���� ���⿼����κ������ۺ����⣬�漰��ԳƵ����ʣ����κ��������ʣ�������Ǻ���������ϵ���������ʽ��֪ʶ�����ݽ�Ϊ�ۺϣ�����ѧ���������֪ʶ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{54}•\sqrt{\frac{1}{2}}=\frac{3}{2}\sqrt{6}$ | B�� | $\sqrt{36}=��6$ | C�� | x4+x4=2x4 | D�� | ��x2y��3=x6y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
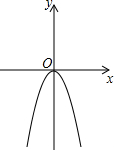 ��ͼ����֪������y=-x2ͨ��ƽ�ƺ�õ�����y1=-��x-1��2+2��y2=-��x-2��2+4��y3=-��x-3��2+6������ƽ�ƺ�Ķ��㡭��P1��P2��P3����Pk��kΪ���������ζ��ڸ���ϣ���Щ�����߳�Ϊ���ö��������ߡ���
��ͼ����֪������y=-x2ͨ��ƽ�ƺ�õ�����y1=-��x-1��2+2��y2=-��x-2��2+4��y3=-��x-3��2+6������ƽ�ƺ�Ķ��㡭��P1��P2��P3����Pk��kΪ���������ζ��ڸ���ϣ���Щ�����߳�Ϊ���ö��������ߡ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����֪������y=ax2-4x-5��a��0��aΪ��������һ�κ���y=$\frac{1}{2}$x+b��bΪ���������ڵ�M��6��n����ֱ��y=$\frac{1}{2}$x+b��x�ἰy�ύ������A��B����AOB���ܳ���12+4$\sqrt{5}$��������y=ax2-4x-5��y�ύ�ڵ�C����x�ύ�ڵ�D��E����E�ڵ�D���Ҳࣩ��
��ͼ��ʾ����֪������y=ax2-4x-5��a��0��aΪ��������һ�κ���y=$\frac{1}{2}$x+b��bΪ���������ڵ�M��6��n����ֱ��y=$\frac{1}{2}$x+b��x�ἰy�ύ������A��B����AOB���ܳ���12+4$\sqrt{5}$��������y=ax2-4x-5��y�ύ�ڵ�C����x�ύ�ڵ�D��E����E�ڵ�D���Ҳࣩ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
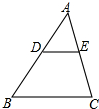 ��ͼ���ڡ�ABC�У�DE��BC����AD=2��DB=3����$\frac{DE}{BC}$=$\frac{2}{5}$��
��ͼ���ڡ�ABC�У�DE��BC����AD=2��DB=3����$\frac{DE}{BC}$=$\frac{2}{5}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com