Question

14．在平面直角坐标系xOy中，对于点P和⊙O给出如下定义：若⊙O上存在两个点A、B，使得∠APB=60°，则称P为⊙O的关联点．
已知点M（$\frac{1}{2}$，-$\frac{1}{2}$），N（-2，0），E（0，-4），F（2$\sqrt{3}$，0）．
（1）当⊙O的半径为1时，①在点M，N，E，F中，⊙O的关联点是M，E；
②过点F作直线l交y轴正半轴于点G，使∠GFO=30°，若直线l上的点P（m，n）是⊙O的关联点，求n的取值范围；
（2）若线段EF上的所有点都是半径为r的⊙O的关联点，求半径r的取值范围．

Answer 1

分析 （1）若点P刚好是⊙O的关联点，则点P到⊙O的两条切线PA与PB之间的夹角为60°，此时OP=2r，进而得到：若点P是⊙O的关联点，则需点P到圆心O的距离d满足0≤d≤2r．
①由于OM＜2，OE=2，OF＞2，因此点M、E是⊙O的关联点；②只需考虑点F刚好是⊙O的关联点时所对应的m的值，就可得到m的取值范围．
（2）由于线段EF任意一点到点O的距离都小于等于OF，因此要使线段EF上的所有点都是⊙O的关联点，只需OF≤2r即可，由OF=2 $\sqrt{3}$即可得到⊙O的半径r的取值范围．

解答 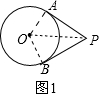解：（1）由题可知：若点P刚好是⊙O的关联点，则点P到⊙O的两条切线PA与PB之间的夹角为60°，如图1，
∵PA、PB与⊙O分别相切于点A、B，
∴∠OAP=∠OBP=90°，∠APO=∠BPO=$\frac{1}{2}$∠APB=30°．
∴OP=2OA．
设⊙O的半径为r，则点P刚好是⊙O的关联点时OP=2r．
所以若点P是⊙O的关联点，则需点P到圆心O的距离d满足0≤d≤2r．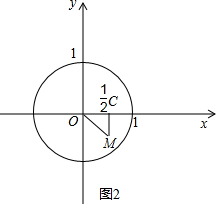
①过点M作MC⊥x轴，垂足为C，连接OM，如图2，
∵点M（ $\frac{1}{2}$，-$\frac{1}{2}$），
∴OC=MC=$\frac{1}{2}$．
∴OM=$\frac{\sqrt{2}}{2}$．
∵0＜OM＜2，OE=2，OF＞2，
∴点M、点E是⊙O的关联点，点F不是⊙O的关联点．
故答案为M、E；
②过点O作OH⊥GF，垂足为H，如图3，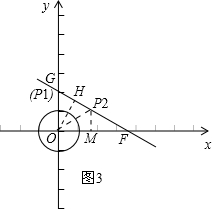

则有OH=$\frac{1}{2}$OF=$\sqrt{3}$．
当点P刚好是⊙O的关联点时，OP=2．
∵OH＜OP，
∴点P刚好是⊙O的关联点的位置有两个，记为P₁、P₂．
在Rt△GOF中，tan∠GFO=$\frac{OG}{OF}$=$\frac{OG}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
解得：OG=2．
所以点P₁与点G重合，此时m=0，n=2，
过点P₂作P₂M⊥x轴，垂足为M，
∵∠OGF=90°-30°=60°，OP₁=OP₂，
∴∠OP₂P₁=∠OP₁P₂=∠OGP₂=60°．
∴∠P₂OF=30°．
∴cos∠P₂OM=$\frac{OM}{O{P}_{2}}$=$\frac{OM}{2}$=$\frac{\sqrt{3}}{2}$．
∴OM=$\sqrt{3}$，此时m=$\sqrt{3}$．n=1，
∵直线l上的点P（m，n）是⊙O的关联点，
∴点P在线段P₁P₂（即GP₂）上，
∴n的范围是1≤n≤2；

（2）由于线段EF任意一点到点O的距离都小于等于OF，
因此要使线段EF上的所有点都是⊙O的关联点，只需OF≤2r，即2 $\sqrt{3}$≤2r，
则有r≥$\sqrt{3}$．
∴⊙O的半径r的取值范围是r≥$\sqrt{3}$．

点评 本题通过新定义，考查了切线的性质、切线长定理、锐角三角函数的定义、等腰三角形的性质、三角形的外角性质、特殊角的三角函数值、勾股定理、30°角所对的直角边等于斜边的一半等知识，考查了阅读理解能力及分析问题解决问题的能力，是一道好题．