
 如图所示:△AOB的三个顶点的坐标分别为O(0,0),A(5,0),B(1,4).
如图所示:△AOB的三个顶点的坐标分别为O(0,0),A(5,0),B(1,4).分析 (1)利用面积公式计算,其中,该三角形的底边长为OA的长,高为点B的纵坐标.
(2)直角坐标系中,一个点的纵坐标减小3个单位,意味着这个点向左平移了三个单位,故将△AOB向右平移三个单位即可.
(3)若O,A两点位置不变,而三角形OAB的面积变为原三角形面积的2倍,就意味着该三角形的高扩大为原来的2倍,求得点B的纵坐标即可解决问题.
解答 解:(1)S△AOB=$\frac{1}{2}×5×4$=10,
即:三角形△AOBDE 面积是10.
(2)如图1: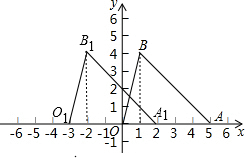
图1
则△O1 A1 B1 为所求作的三角形.
O1,A1,B1的坐标分别为:
O1(-3,0)A1(2,0)B1(-2,4)
(3)因为,设BD为△OAB的高,
则:S△OAB=$\frac{1}{2}$OA|BD|=2S△AOB|BD|=8,
∴BD=8,
∴点B的纵坐标为±8,
∴当点B在直线y=8或直线y=-8上时,三角形OAB的面积是原三角形面积的2倍.
点评 本题考查了平移作图、直角坐标系等知识点,解题的关键是理解坐标系中点的坐标的意义及平移变化时坐标的变化规律.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知中心线的两个半圆弧半径都为1000mm,两直管道的长度都为2000mm,求图中管道的展直长度(即图中虚线所表示的中心线的长度,精确到1mm)
如图,已知中心线的两个半圆弧半径都为1000mm,两直管道的长度都为2000mm,求图中管道的展直长度(即图中虚线所表示的中心线的长度,精确到1mm)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com