
 与
与 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥ 轴),并且分别与
轴),并且分别与 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
 范围内)时,S最大值=50.
范围内)时,S最大值=50. FD=
FD= t. 又AP=3t.
t. 又AP=3t. t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2= t2,AP2=3t2;
t2,AP2=3t2; ,又∠A=∠A,∴△AF1P1∽△AF2P2.
,又∠A=∠A,∴△AF1P1∽△AF2P2. 与
与 轴、
轴、 轴分别交于A、B两点
轴分别交于A、B两点 (OP+EF)·OE=18.
(OP+EF)·OE=18. (OP+EF)·OE=
(OP+EF)·OE= (20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50.
(20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50. 范围内)时,S最大值="50."
范围内)时,S最大值="50." 

|
 (3) 作FD⊥x轴于D,则四边形OEFD为矩形.
(3) 作FD⊥x轴于D,则四边形OEFD为矩形. ∴FD=OE=t,AF=
∴FD=OE=t,AF= FD=
FD= t. 又AP=3t.
t. 又AP=3t. t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2= t2,AP2=3t2;
t2,AP2=3t2; ,又∠A=∠A,∴△AF1P1∽△AF2P2.
,又∠A=∠A,∴△AF1P1∽△AF2P2.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:不详 题型:单选题
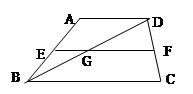
| A.3 | B.6 | C.8 | D.12 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
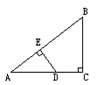
| A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
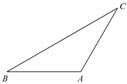
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.10 cm | B.12 cm | C.14 cm | D.16 cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com