
分析 根据分式的额加减法和除法可以化简题目中的式子,再根据x2-2$\sqrt{3}$x+a=0有两个不相等的实数根,且a为非负整数和求得的a的值必须使得原分式有意义,从而可以求得a的值,然后代入化简后的式子即可解答本题.
解答 解:$\frac{a-3}{3{a}^{2}-6a}$÷(a+2-$\frac{6a-13}{a-2}$)
=$\frac{a-3}{3a(a-2)}÷\frac{(a+2)(a-2)-(6a-13)}{a-2}$
=$\frac{a-3}{3a(a-2)}•\frac{a-2}{{a}^{2}-4-6a+13}$
=$\frac{a-3}{3a}•\frac{1}{{a}^{2}-6a+9}$
=$\frac{a-3}{3a}•\frac{1}{(a-3)^{2}}$
=$\frac{1}{3{a}^{2}-9a}$,
∵x2-2$\sqrt{3}$x+a=0有两个不相等的实数根,且a为非负整数,
∴△=$(-2\sqrt{3})^{2}-4×1×a>0$且a≥0,a为整数,
解得,0≤a<3且a为整数,
∵a-2≠0,a≠0,
∴a=1,
当a=1时,原式=$\frac{1}{3×{1}^{2}-9×1}=-\frac{1}{6}$.
点评 本题考查分式的化简求值、根的判别式,解答本题的关键是明确分式化简求值的方法,利用根的判别式解答.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
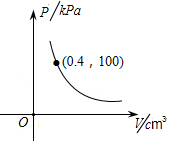 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(Kpa)是气体体积V(cm3)的反比例函数,其图象如图所示,当气球内气压大于120Kpa时,气球将爆炸,为了安全,该气球内气体体积V(cm3)的取值范围是V≥$\frac{1}{3}$.
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(Kpa)是气体体积V(cm3)的反比例函数,其图象如图所示,当气球内气压大于120Kpa时,气球将爆炸,为了安全,该气球内气体体积V(cm3)的取值范围是V≥$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
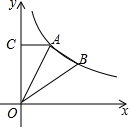 如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).
如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com