
| A. | 中位数是10 | B. | 众数是10 | C. | 平均数是9.5 | D. | 方差是16 |
分析 排序后位于中间或中间两数的平均数即为中位数;一组数据中出现次数最多的数据叫做众数;平均数是指在一组数据中所有数据之和再除以数据的个数;一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.
解答 解:(A)中位数为$\frac{9+10}{2}$=9.5,故(A)错误;
(B)根据出现次数最多的数据是10可得,众数是10,故(B)正确;
(C)平均数为(10+6+9+11+8+10)÷6=9,故(C)错误;
(D)方差为$\frac{1}{6}$[(10-9)2+(6-9)2+(9-9)2+(11-9)2+(8-9)2+(10-9)2]=$\frac{8}{3}$,故(D)错误.
故选B.
点评 本题主要考查了极差、众数、平均数以及方差的计算,注意:极差只能反映数据的波动范围,众数反映了一组数据的集中程度,平均数是反映数据集中趋势的一项指标,方差是反映一组数据的波动大小的一个量.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 8.9 | 9.3 | 9.4 | 9.5 | 9.7 | 9.8 |
| 评委(名) | 1 | 2 | 1 | 4 | 1 | 1 |
| A. | 9.3,2 | B. | 9.5,4 | C. | 9.5,9.5 | D. | 9.4,9.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
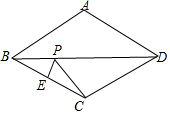 如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )
如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数 | 3 | 4 | 2 | 1 |
| 答对题数 | 4 | 5 | 7 | 8 |
| A. | 4和5 | B. | 5和4 | C. | 5和5 | D. | 6和5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
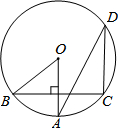 如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,∠ADC=26°,那么∠AOB的度数为( )
如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,∠ADC=26°,那么∠AOB的度数为( )| A. | 64° | B. | 26° | C. | 52° | D. | 38° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
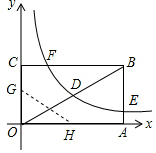 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=$\frac{1}{2}$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=2 | B. | a=-3,b=2 | C. | a=3,b=-2 | D. | a=-3,b=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com