
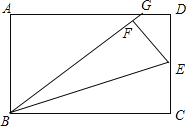
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
【答案】![]()
【解析】
连接GE,根据中点定义可得DE=CE,再根据翻折的性质可得DE=EF,∠BFE=90°,利用“HL”证明Rt△EDG≌Rt△EFG,根据全等三角形对应边相等可得FG=DG,根据![]() ,设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,由勾股定理求得AB=
,设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,由勾股定理求得AB=![]() ,再求比值即可.
,再求比值即可.
连接GE,
∵点E是CD的中点,∴EC=DE,
∵将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,
∴EF=DE,∠BFE=90°,
在Rt△EDG和Rt△EFG中![]() ,
,
∴Rt△EDG≌Rt△EFG(HL),
∴FG=DG,
∵![]() ,
,
∴设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,
∴AB=![]() ,
,
故![]() ,
,
故答案为:![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名同学参加少年科技创新选拔赛,六次比赛的成绩如下:
甲:87 93 88 93 89 90
乙:85 90 90 96 89 ![]()
(1)甲同学成绩的中位数是__________;
(2)若甲、乙的平均成绩相同,则![]() __________;
__________;
(3)已知乙的方差是![]() ,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.
,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
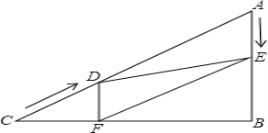
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个动点到达终点时,另一个动点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)当t为何值时,DF=DA?
(2)当t为何值时,△ADE为直角三角形?请说明理由.
(3)是否存在某一时刻t,使点F在线段AC的中垂线上,若存在,请求出t值,若不存在,请说明理由.
(4)请用含有t式子表示△DEF的面积,并判断是否存在某一时刻t,使△DEF的面积是△ABC面积的![]() ,若存在,请求出t值,若不存在,请说明理由.
,若存在,请求出t值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
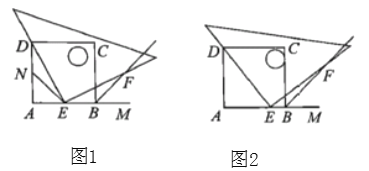
【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 是正方形,
是正方形,![]() 是
是![]() 延长线上一点,直角三角尺的一条直角边经过点
延长线上一点,直角三角尺的一条直角边经过点![]() ,且直角顶点
,且直角顶点![]() 在
在![]() 边上滑动(点
边上滑动(点![]() 不与点
不与点![]() 重合),另一条直角边与
重合),另一条直角边与![]() 的平分线
的平分线![]() 相交于点
相交于点![]() .
.
(1)如图1所示,当点![]() 在
在![]() 边的中点时:
边的中点时:
①通过测量![]() 的长度,猜想
的长度,猜想![]() 与
与![]() 满足的数量关系是________________;
满足的数量关系是________________;
②连接点![]() 与
与![]() 边的中点
边的中点![]() ,猜想
,猜想![]() 与
与![]() 满足的数量关系是________________;
满足的数量关系是________________;
③请证明上述你的两个猜想.
(2)如图2所示,当点![]() 在
在![]() 边上的任意位置时,请你在
边上的任意位置时,请你在![]() 边上找到一点
边上找到一点![]() ,使得
,使得![]() ,进而猜想此时
,进而猜想此时![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在11月中旬对甲、乙、丙三种型号的电视机进行促销.其中,甲型号电视机直接按成本价1280元的基础上获利![]() 定价;乙型号电视机在原销售价2199元的基础上先让利199元,再按八五折优惠;丙型号电视机直接在原销售价2399元上减499元;活动结束后,三种型号电视机总销售额为20600元,若在此次促销活动中,甲、乙、丙三种型号的电视机至少卖出其中两种型号,则三种型号的电视机共______有种销售方案.
定价;乙型号电视机在原销售价2199元的基础上先让利199元,再按八五折优惠;丙型号电视机直接在原销售价2399元上减499元;活动结束后,三种型号电视机总销售额为20600元,若在此次促销活动中,甲、乙、丙三种型号的电视机至少卖出其中两种型号,则三种型号的电视机共______有种销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水晶厂生产的水晶工艺品非常畅销,某网店专门销售这种工艺品.成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当x=40时,y=300;当x=55时,y=150.
(1)求y与x之间的函数关系式;
(2)如果规定每天工艺品的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该工艺品销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(10.0)及在第一象限的动点P(x,y),且x+y=12,设△OPA的面积为S。
(1)求S关于x的函数解析式;
(2)求x的取值范围;
(3)当S=15时,求P点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市购进一种水果进行销售,购进情况和销售情况见下表:
项目 | 购进资金 单位:元 | 进货价 单位:元/kg | 销售定价 单位:元/kg | 销售情况 | 水果重量 单位:kg |
第一次 | 6000 | m | 16 | 按定价全部售完 | 第二次是第一次的两倍 |
第二次 | 13000 | m+1 | 16 | 按定价售出一部分后,余下的400kg按定价的7折售完 |
(1)第二次的进货价是多少元/kg?
(2)超市在这两次销售中共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com