
【题目】如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.
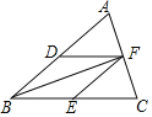
(1)求证:四边形BEFD是平行四边形;
(2)若∠AFB=90°,AB=4,求四边形BEFD的周长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
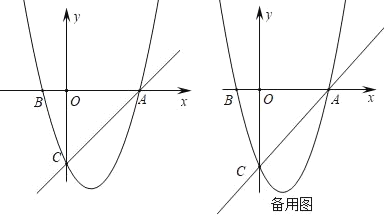
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)求抛物线的解析式;
(2)若动点P在第四象限内的抛物线上,过动点P作x轴的垂线交直线AC于点D,交x轴于点E,垂足为E,求线段PD的长,当线段PD最长时,求出点P的坐标;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
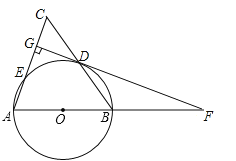
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=![]() ,求CG的长.
,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
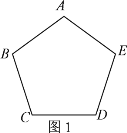
【题目】数学中我们学习了尺规作图,小明发现有些作图只用一种工具就可以完成,你能解决下列问题吗?
(1)请只用无刻度的直尺完成下列作图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果)在图1中,过点A画一条直线把正五边形ABCDE分成面积相等的两部分;
(2)已知直线l及l外一点A(按下列要求作图,不写画法,保留画图痕迹).
①在图2中,只用圆规在直线l上画出两点B、C,使得点A、B、C是一个等腰三角形的三个顶点;
②在图3中,只用圆规在直线l外画出一点P,使得点A、P所在直线与直线l平行.
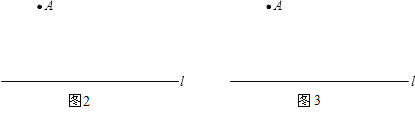
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
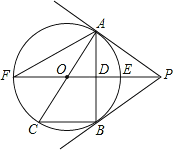
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点![]() ,经过点
,经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
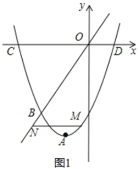
(1)求该抛物线的解析式;
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
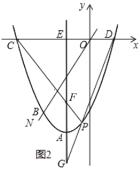
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,直线
之间的一个动点,直线![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() ,当点
,当点![]() 运动时.
运动时.
①直接写出![]() 的值;
的值;
②直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城共有肥料500吨,其中A城肥料比B城肥料少100吨,从A,B城往C,D两乡运肥料的平均费用如表:
A城 | B城 | |
C乡 | 20元/吨 | 15元/吨 |
D乡 | 25元/吨 | 30元/吨 |
现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从B城运往D乡x吨肥料,总运费为y元,求y与x之间的函数关系,并说明如何安排运输才能使得总运费最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com