【答案】
分析:①连接OA,OC,过O作OD⊥AC于D,求出CD、AD,由勾股定理求出OD,求出∠ACO推出∠AOC=120°,根据圆周角定理求出∠B=

∠AOC,代入求出即可.②同样可求出∠D=60°,根据圆内接四边形性质求出∠ABC=120°.
解答:解:如图1,
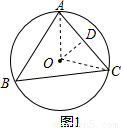
连接OA,OC,过O作OD⊥AC于D,
∵OD⊥AC,OD过圆心O,
∴AD=CD=

AC=3
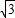
,
由勾股定理得:OD=
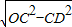
=
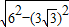
=3,
即OD=

OC,
∴∠DCO=30°,∠COD=60°,
同理∠AOD=60°,
∵∠B=

∠AOC,
∴∠B=60°.
②如图2
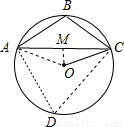
∵由垂径定理得CM═3
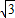
,OC=6,由勾股定理得:OM=3,
∴∠OCM=30°,∴∠MOC=60°,
∴∠AOC=2∠MOC=120°,
由圆周角定理得:∠D=60°,
∵A、D、C、B四点共圆,
∴∠ABC=120°,
故答案为:60°或120°.
点评:本题考查了垂径定理,圆周角定理,勾股定理,含30度角的直角三角形,三角形的外接圆等知识点的应用,关键是求出∠AOC的度数,通过做此题培养了学生的推理能力和计算能力.

 cm,则∠B等于______.
cm,则∠B等于______. ∠AOC,代入求出即可.②同样可求出∠D=60°,根据圆内接四边形性质求出∠ABC=120°.
∠AOC,代入求出即可.②同样可求出∠D=60°,根据圆内接四边形性质求出∠ABC=120°.
 AC=3
AC=3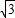 ,
,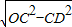 =
=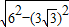 =3,
=3, OC,
OC, ∠AOC,
∠AOC,
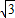 ,OC=6,由勾股定理得:OM=3,
,OC=6,由勾股定理得:OM=3,
