
【题目】圆柱形纸筒沿母线AB剪开铺平,得到一个矩形(如图).如果将这个纸筒沿线路BMA剪开铺平,得到的图形是( )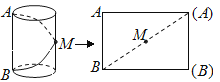
A.矩形
B.半圆
C.三角形
D.平行四边形
【答案】D
【解析】严格按照图中的方法亲自动手操作一下,即可很直观地呈现出来.
M是所在母线的中点,如果将这个纸筒沿线路BMA剪开,即把圆柱延AB与M所在母线平方在一个平面内,再剪开AM,BM.则得到两个重合的△ABM,△ABM是等腰三角形,且AB是底边,展开后得到的图形是一个以△ABM的腰AM、BM为边的四边形,相对的边对应相等,所以是平行四边形.
故选D.
【考点精析】通过灵活运用平行四边形的判定,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.

(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,Rt△ABC中,∠ACB=90°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(2)如图2,在△ABC中,∠ACB=40°,点D、E在直线AB上,且AD=AC,BE=BC,则∠DCE的度数;
(3)在△ABC中,∠ACB=n°(0<n<180°),点D、E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案,用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一个平行四边形ABCD,其中H、G两点分别在BC、CD上,AH⊥BC,AG⊥CD,且AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4四个角.若AH=5,AG=6,则下列关系何者正确( )
A.∠1=∠2
B.∠3=∠4
C.BH=GD
D.HC=CG
查看答案和解析>>
科目:初中数学 来源: 题型:
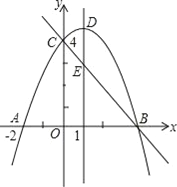
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明“在一个三角形中不能有两个内角为直角”,首先应假设( )
A. 在一个三角形中有两个内角为直角
B. 在一个三角形中不能有两个内角为直角
C. 所有的三角形中不能有两个内角为直角
D. 一个三角形中有三个内角是直角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.

(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com