
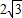 ,D、E两点分别在AC、BC上,且DE∥AB,CD=
,D、E两点分别在AC、BC上,且DE∥AB,CD=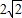 .将△CDE绕点C顺时针旋转,得到△CD′E′(如图②,点D′、E′分别与点D、E对应),点E′在AB上,D′E′与AC相交于点M.
.将△CDE绕点C顺时针旋转,得到△CD′E′(如图②,点D′、E′分别与点D、E对应),点E′在AB上,D′E′与AC相交于点M.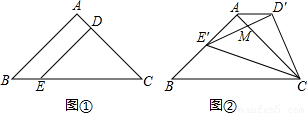
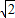 ,
,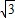 ,CE′=4,
,CE′=4,
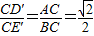 ,
,
 ,
,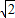 ,∠FCD′=30°,
,∠FCD′=30°,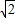 ,
,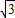 .
.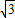 ,SRt△D′E′C=4.(10分)
,SRt△D′E′C=4.(10分)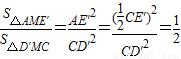 .(11分)
.(11分) S△CD′M.
S△CD′M. ,
,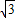 ,
,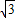 ,
,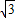 -5.
-5.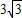 -5.(12分)
-5.(12分)

科目:初中数学 来源:2007年全国中考数学试题汇编《四边形》(01)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(河上镇中 董勇) (7)(解析版) 题型:填空题
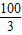 ,它的对角线OB与双曲线
,它的对角线OB与双曲线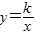 相交于点D,且OB:OD=5:3,则k= .
相交于点D,且OB:OD=5:3,则k= .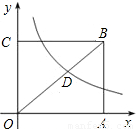
查看答案和解析>>
科目:初中数学 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(瓜沥一中 沈海虹)(解析版) 题型:填空题
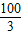 ,它的对角线OB与双曲线
,它的对角线OB与双曲线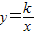 相交于点D,且OB:OD=5:3,则k= .
相交于点D,且OB:OD=5:3,则k= .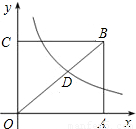
查看答案和解析>>
科目:初中数学 来源:2007年江苏省南通市中考数学试卷(解析版) 题型:填空题
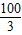 ,它的对角线OB与双曲线
,它的对角线OB与双曲线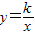 相交于点D,且OB:OD=5:3,则k= .
相交于点D,且OB:OD=5:3,则k= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com