
| 第一列 | 第二列 | 第三列 | 第四列 | ||
| 第一行 | 0 | 2 | 4 | 6 | … |
| 第二行 | 2 | 4 | 6 | 8 | … |
| 第三行 | 4 | 6 | 8 | 10 | … |
| 第四行 | 6 | 8 | 10 | 12 | … |
| … | … | … | … | … |
分析 由题意可知:第1行与第1列的交叉点上的数应为2×2×(1-1)=0;第2行与第2列的交叉点上的数应为2×2×(2-1)=4;第3行与第3列的交叉点上的数应为2×2×(3-1)=8;…由此得出第n行与第n列的交叉点上的数应为4(n-1),由此规律求得答案即可.
解答 解:∵第1行与第1列的交叉点上的数应为2×2×(1-1)=0;
第2行与第2列的交叉点上的数应为2×2×(2-1)=4;
第3行与第3列的交叉点上的数应为2×2×(3-1)=8;
…
∴第n行与第n列的交叉点上的数应为4(n-1),
∴第6行与第6列的交叉点上的数应为20.
故答案为:20,4(n-1),.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题,最后要注意验证所找出的规律的正确性.


科目:初中数学 来源: 题型:解答题
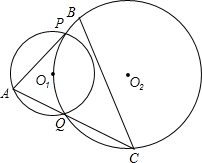 如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心.
如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
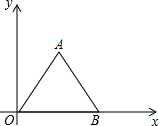 在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)
在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com