
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]()
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m, ![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
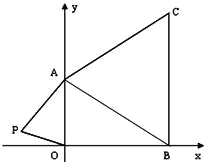
【答案】(1)a=2,b=3,c=4;
(2)S四边形ABOP=3-m;
(3)存在m=-3,P(-3, ![]() )
)
【解析】试题分析:(1)用非负数的性质求解;(2)把四边形ABOP的面积看成两个三角形面积和,用m来表示;(3)△ABC可求,是已知量,根据题意,方程即可.
试题解析:(1)由已知![]() ,
,
可得:a=2,b=3,c=4;
(2)∵S△ABO=![]() ×2×3=3,S△APO=
×2×3=3,S△APO=![]() ×2×(m)=m,
×2×(m)=m,
∴S四边形ABOP=S△ABO+S△APO=3+(m)=3m
(3)因为S△ABC=![]() ×4×3=6,
×4×3=6,
∵S四边形ABOP=S△ABC
∴3m=6,
则m=3,
所以存在点P(3, ![]() )使S四边形ABOP=S△ABC.
)使S四边形ABOP=S△ABC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】由a+3=b变为2(a+3)-5=2b-5,其过程中所用等式的性质及顺序是( )
A. 先用等式的性质1,再用等式的性质2
B. 先用等式的性质2,再用等式的性质1
C. 仅用了等式的性质1
D. 仅用了等式的性质2
查看答案和解析>>
科目:初中数学 来源: 题型:
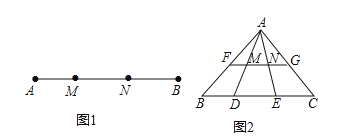
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=Rt∠,直角边AB、BC的长(AB<BC)是方程![]() 2-7
2-7![]() +12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
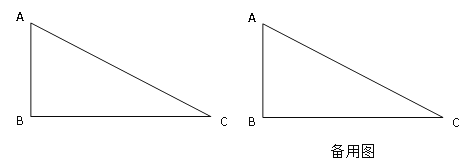
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为![]() 时运动时间t的值;
时运动时间t的值;
(3)点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )
A. y=(x﹣1)2+2 B. y=(x﹣1)2+3
C. y=(x﹣2)2+2 D. y=(x﹣2)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度每秒,点B和C运动的速度是3个单位长度每秒.设三个点运动的时间为t秒(t≠5),设线段OA的中点为P,线段OB的中点为M,线段OC的中点为N,当2PM-PN=2时,t的值为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)某种电子产品共![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品 件;
(2)如果从中任意取出![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com