
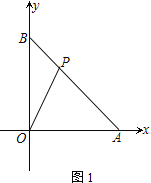
【题目】如图1,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点
(1) 如图1,若S△AOP=12,求P的坐标
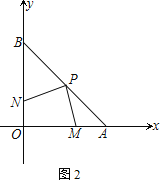
(2) 如图2,若P为AB的中点,点M、N分别是OA、OB边上的动点,点M从顶点A、点N从顶点O同时出发,且它们的速度都为1 cm/s,则在M、N运动的过程中,线段PM、PN之间有何关系?并证明
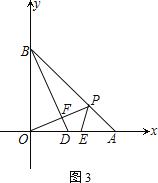
(3) 如图3,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP,交OP、OA分别与F、D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由
【答案】(1)P(2,4);(2)PM=PN,PM⊥PN,理由见解析;(3)OD=AE,理由见解析
【解析】试题分析:(1)如图1中,作PH⊥OA于H.线求出直线AB的解析式,利用面积构建方程求出PH即可解决问题;
(2)结论:PM=PN,PM⊥PN.连接OP.只要证明△PON≌△PAM即可解决问题;
(3)结论:OD=AE.如图3中,作AG⊥x轴交OP的延长线于G.由△DBO≌△GOA,推出OD=AG,∠BDO=∠G,再证明△PAE≌△PAG即可解决问题;
试题解析:解:(1)如图1中,作PH⊥OA于H.
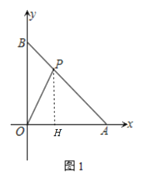
∵A(6,0),B(0,6),∴直线AB的解析式为y=﹣x+6.∵ ![]() OAPH=12,∴PH=4,当y=4时,4=﹣x+6,∴x=2,∴P(2,4).
OAPH=12,∴PH=4,当y=4时,4=﹣x+6,∴x=2,∴P(2,4).
(2)结论:PM=PN,PM⊥PN.证明如下:
如图2中,连接OP.
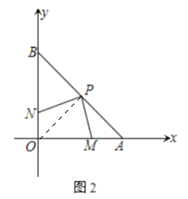
∵OB=OA,∠AOB=90°,PB=PA,∴OP=PB=PA,OP⊥AB,∠PON=∠A=45°,∴∠OPA=90°.
∵AM=ON,OP=OP,∴△PON≌△PAM,∴PN=PM,∠OPN=∠APM,∴∠NPM=∠OPA=90°,
∴PM⊥PN,PM=PN.
(3)结论:OD=AE.理由如下:
如图3中,作AG⊥x轴交OP的延长线于G.

∵BD⊥OP,∴∠OAG=∠BOD=∠OFD=90°,∴∠ODF+∠AOG=90°,∠ODF+∠OBD=90°,∴∠AOG=∠DBO,∵OB=OA,∴△DBO≌△GOA,∴OD=AG,∠BDO=∠G.∵∠BDO=∠PEA,∴∠G=∠AEP.∵∠PAE=∠PAG=45°,PA=PA,∴△PAE≌△PAG,∴AE=AG,∴OD=AE.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A(﹣2,3),B(﹣3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( ) 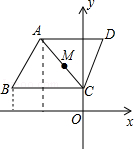
A.(﹣2017,2)
B.(﹣2017,﹣2)
C.(﹣2018,﹣2)
D.(﹣2018,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图①,△ABC、△AED是两个全等的等腰直角三角形(其顶点B、E重合),∠BAC=∠AED=90°,O为BC的中点,F为AD的中点,连接OF.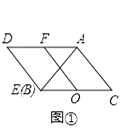
(1)问题发现
①如图①,线段OF与EC的数量关系为;
②将△AED绕点A逆时针旋转45°,如图②,OF与EC的数量关系为;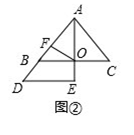
(2)类比延伸
将图①中△AED绕点A逆时针旋转到如图③所示的位置,请判断线段OF与EC的数量关系,并给出证明.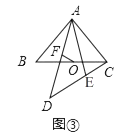
(3)拓展探究
将图①中△AED绕点A逆时针旋转,旋转角为α,0°≤α≤90°,AD= ![]() ,△AED在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长.
,△AED在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为56,则n=_.
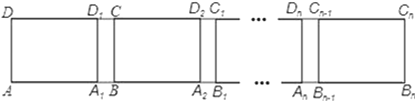
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED= °
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
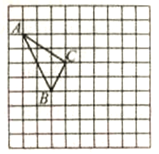
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为A(-4,5),C(-1,3).
(1)请在网格平面内作出平面直角坐标系(不写作法);
(2)请作出△ABC关于y轴对称△A'B'C';
(3)分别写出A'、B'、C'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组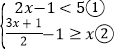
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com