
����Ŀ�� �ڽ������������ũ������У�ij��ί����Ͷ�ʿ�����Ŀ������6����Ŀ�ɹ�ѡ����Ŀ�����ʽ�Ԥ�����������±���
�����ʽ���Ԫ�� | 1 | 2 | 4 | 6 | 7 | 8 |
Ԥ������ǧ��Ԫ�� | 0.2 | 0.35 | 0.55 | 0.7 | 0.9 | 1 |
��1���ϱ���ӳ������������֮��Ĺ�ϵ���ĸ����Ա������ĸ����������
��2�����Ԥ��Ҫ���0.9ǧ��Ԫ���������������Ͷ����Ŀ��
��3������ô�����ó�10��Ԫ���ж����Ŀ��Ͷ�ʣ�Ԥ������������Ƕ��٣�˵�����ɣ�
���𰸡���1�������ʽ������֮��Ĺ�ϵ�������ʽ�Ϊ�Ա�����������Ϊ���������2������Ͷ��һ��7��Ԫ����Ŀ��Ҳ����Ͷ��һ��2��Ԫ����Ͷ��һ��4��Ԫ����Ŀ��������Ͷ��һ��1��Ԫ����Ͷ��һ��6��Ԫ����Ŀ����3�����������1.45��Ԫ���������������
��������
��1���ֱ���ݱ�����������Ķ���ֱ�ó����ɣ�
��2������ͼ�������ó�Ͷ�ʷ�����
��3���ֱ������ͬ��������������ó��𰸣�
�⣺��1�������ʽ������֮��Ĺ�ϵ��
�����ʽ�Ϊ�Ա�����������Ϊ�������
��2������Ͷ��һ��7��Ԫ����Ŀ��
Ҳ����Ͷ��һ��2��Ԫ����Ͷ��һ��4��Ԫ����Ŀ��
������Ͷ��һ��1��Ԫ����Ͷ��һ��6��Ԫ����Ŀ��
�𣺿���Ͷ��һ��7��Ԫ����Ŀ��Ҳ����Ͷ��һ��2��Ԫ����Ͷ��һ��4��Ԫ����Ŀ��������Ͷ��һ��1��Ԫ����Ͷ��һ��6��Ԫ����Ŀ��
��3�������ַ�������1��Ԫ��2��Ԫ��7��Ԫ��������![]() ��Ԫ��
��Ԫ��
��2��Ԫ��8��Ԫ��������![]() ��Ԫ��
��Ԫ��
��4��Ԫ��6��Ԫ��������![]() ��Ԫ��
��Ԫ��
�����������![]() ��Ԫ��
��Ԫ��
�����������![]() ��Ԫ��
��Ԫ��


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ڼס��������ֿ�ֱ���ũ�ó�![]() ����
����![]() ��������Ҫ����
��������Ҫ����![]() ��
��![]() ���� ����
���� ����![]() ��
��![]() ������֪�Ӽײֿ����һ��ũ�ó���
������֪�Ӽײֿ����һ��ũ�ó���![]() �غ�
�غ�![]() �ص��˷ѷֱ�Ϊ
�ص��˷ѷֱ�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ�����Ҳֿ����һ��ũ�ó���
Ԫ�����Ҳֿ����һ��ũ�ó���![]() �غ�
�غ�![]() �ص��˷ѷֱ�Ϊ
�ص��˷ѷֱ�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ���Ӽײֿ����
Ԫ���Ӽײֿ����![]() ��ũ�ó�
��ũ�ó�![]() ����
����
![]() �ײֿ����
�ײֿ����![]() ��ũ�ó�____ �����Ҳֿ����
��ũ�ó�____ �����Ҳֿ����![]() ��ũ�ó� _�����Ҳֿ����B��ũ�ó�____ ��(�ú�
��ũ�ó� _�����Ҳֿ����B��ũ�ó�____ ��(�ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
![]() д����˾�Ӽס��������ֿ��ũ�ó���
д����˾�Ӽס��������ֿ��ũ�ó���![]() ��
��![]() ��������Ҫ�����˷�(�ú�
��������Ҫ�����˷�(�ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
![]() ��
��![]() �Ļ����ϣ������˷���
�Ļ����ϣ������˷���Ԫʱ���Ӽײֿ����
![]() ��ũ�ó�������?
��ũ�ó�������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
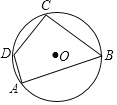
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��AB=17��CD=10����A=90�㣬cosB=![]() ����AD�ij���
����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
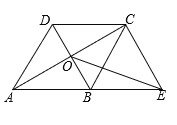
����Ŀ�����ı���ABCD�У�AB��DC��AB=AD���Խ���AC��BD���ڵ�O��ACƽ�֡�BAD������C��CE��DB��AB���ӳ����ڵ�E������OE��
��1����֤���ı���ABCD�����Σ�
��2������DAB=60������AB=4����OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
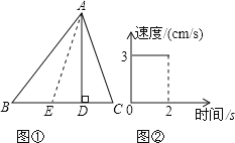
����Ŀ�� ��ͼ����ʾ������ABC�У�AD�������εĸߣ���AD=6cm��E��һ�����㣬��B��C�ƶ������ٶ���ʱ��ı仯��ϵ��ͼ����ʾ����֪BC=8cm
��1����ͼ�ڣ�E���˶���ʱ��Ϊ______s���ٶ�Ϊ______cm/s
��2����E�����˶���������ABE�����y���˶�ʱ��x֮��Ĺ�ϵʽ��
��3����E��ֹͣ������ABE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��E��F��B��ͬһֱ���ϣ���A��D��BC��࣬AB��CD��AE=DF����A=��D��
��1����֤��AB=CD��
��2����AB=CF����B=30��������D�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪���κ���y=ax2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C�Գ���Ϊֱ��x=1��ֱ��y=��x+c��������y=ax2+bx+c����C��D���㣬D����x���·��Һ�����С��3�������н��ۣ�
��2a+b+c��0����a��b+c��0����x��ax+b����a+b����a����1��
������ȷ���У�������
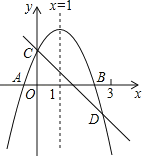
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС����ѧϰ�˺���������ͼ���֪ʶ�������ô�֪ʶ��̽���ܳ�һ���ľ�����߳��ֱ�Ϊ����ʱ������. �뽫���ǵ�̽�����̲�������.
��1���к�������ʽ�������ε��ܳ�Ϊ8������ε�һ�߳�Ϊx�����Ϊy������y=____________��
��2��������������ʽ�У��Ա���x��ȡֵ��Χ��____________��
��3�����
x | �� | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | �� |
y | �� | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | �� |
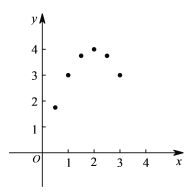
�m=____________��
��4����ͼ����ƽ��ֱ������ϵ����������ϱ��в��ָ���ӦֵΪ����ĵ㣬���㻭���ú�����ͼ��
��5�����ͼ��ɵã�x=____________ʱ�����ε�������д���ú������������ʣ�һ�����ɣ���____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��y=kx+b��y���ڵ�A��0��1������x���ڵ�B��3��0��.ƽ����y���ֱ��x=1��AB�ڵ�D����x���ڵ�E����P��ֱ��x=1��һ���㣬���ڵ�D���Ϸ�����P��1��n��.
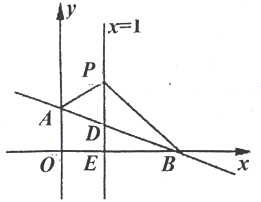
��1����ֱ��AB�ı���ʽ��
��2������ABP��������ú�n�Ĵ���ʽ��ʾ����
��3����S��ABP=2ʱ����PBΪ���ڵ�һ����������ֱ��������BPC��ֱ��д����C������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com