
 ��ͼ����������ABCD�У��Խ���AC��BD���ڵ�O������һ���㹻���ֱ�����ǰ��ֱ�Ƕ������O�غϣ���ֱ�����ǰ����ŵ�O��תʱ������ֱ�DZ�OP��OQ�ֱ𱣳����AB����BC�ཻ�ڵ�E��F������EF�����н��ۣ���EF=OB����EF=$\sqrt{2}$OF���۵�EF��ACʱ����BEF���ܳ���С���ܵ�BE�仯ʱ���ı���OEBF�����Ҳ��֮�仯�����н�����ȷ�ĸ���Ϊ��������
��ͼ����������ABCD�У��Խ���AC��BD���ڵ�O������һ���㹻���ֱ�����ǰ��ֱ�Ƕ������O�غϣ���ֱ�����ǰ����ŵ�O��תʱ������ֱ�DZ�OP��OQ�ֱ𱣳����AB����BC�ཻ�ڵ�E��F������EF�����н��ۣ���EF=OB����EF=$\sqrt{2}$OF���۵�EF��ACʱ����BEF���ܳ���С���ܵ�BE�仯ʱ���ı���OEBF�����Ҳ��֮�仯�����н�����ȷ�ĸ���Ϊ��������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� ������ת�������Լ������ε����ʣ��ɵá�BOE�ա�COF�������ɵá�EOF�ǵ���ֱ�������Σ�S��BOE=S��COF�������ó��ı���OEBF�����=S��BOE+S��BOF=S��COF+S��BOF=S��BOC���Ƕ�ֵ�����ݴ˿ɵ���ȷ�Ľ��ۣ�
��� 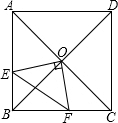 �⣺��EF=OB��һ��������
�⣺��EF=OB��һ��������
��OE��AB��OF��BCʱ���ı���OEBF�������Σ�
��ʱEF=OB��
��OE��AB��OF��BC��һ��������
�ʢٴ���
�ڸ���������ABCD���ɵá�BOC=��EOF=90�㣬OB=OC����OBE=��OCF=45�㣬
���BOE=��COF��
���BOE�ա�COF��
��OE=OF��
���EOF�ǵ���ֱ�������Σ�
��EF=$\sqrt{2}$OF��
�ʢ���ȷ��
���ɢڿɵã���BOE�ա�COF��
��BE=CF��
��BE+BF=CF+BE=BC����ֵ����
�൱EF���ʱ����BEF���ܳ���С��
��ʱOE��OF��̣���OE��AB��OF��BC��
���BEF=��BFE=45�㣬
��EF��AC��
�ʢ���ȷ��
�ܵ�BE�仯ʱ���ı���OEBF��������䣬
�ɢڿɵã���BOE�ա�COF��
��S��BOE=S��COF��
���ı���OEBF�����=S��BOE+S��BOF=S��COF+S��BOF=S��BOC����ֵ����
�ʢܴ���
��ѡ��B��
���� ������Ҫ�����������ε����ʣ���ת�������Լ�ȫ�������ε��ж������ʵ��ۺ�Ӧ�ã��������Ĺؼ�������ȫ�������ε��ж������ʣ�����ʱע�⣺ȫ�������ε������ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�������Ӱڳɵġ�H���֣��ڳɵ�һ����H������Ҫ7ö���ӣ��ڵ�x����H������Ҫ�����������ú�x�Ĵ���ʽ��ʾΪ��������
��ͼ�������Ӱڳɵġ�H���֣��ڳɵ�һ����H������Ҫ7ö���ӣ��ڵ�x����H������Ҫ�����������ú�x�Ĵ���ʽ��ʾΪ��������| A�� | 5x | B�� | 5x-1 | C�� | 5x+2 | D�� | 5x+5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
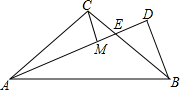 ��ͼ��Rt��ABC�У�AC=BC����ACB=90�㣬��AEΪ��BAC�Ľ�ƽ���ߣ�BD��AE������ΪD��
��ͼ��Rt��ABC�У�AC=BC����ACB=90�㣬��AEΪ��BAC�Ľ�ƽ���ߣ�BD��AE������ΪD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
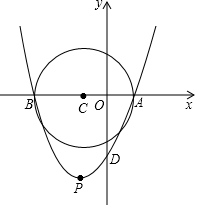 ��ͼ����֪��C��Բ����x���ϣ��ҽ���A��1��0����B��-3��0�����㣬������y=ax2+bx+c��a��0������A��B���㣬����ΪP��
��ͼ����֪��C��Բ����x���ϣ��ҽ���A��1��0����B��-3��0�����㣬������y=ax2+bx+c��a��0������A��B���㣬����ΪP���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com