
【题目】如图,△ABC 内接于⊙O,∠B=60°,CD 是⊙O 的直径,点 P 是 CD 延长线上的一点且 AP=AC.

(1)求证:PA 是⊙O 的切线;
(2)若![]() ,
,![]() ,求⊙O的半径
,求⊙O的半径
【答案】(1)详见解析;(2)3
【解析】
(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,再由AP=AC得出∠P=30°,继而由∠OAP=∠AOC-∠P,可得出OA⊥PA,从而得出结论;
(2)过点C作CE⊥AB于点E.在Rt△BCE中,∠B=60°,BC=4,于是得到BE=![]() BC=2,CE=
BC=2,CE=![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,于是得到AP=AC=
,于是得到AP=AC=![]() .在Rt△PAO中,解直角三角形即可得到结论.
.在Rt△PAO中,解直角三角形即可得到结论.
(1)证明:连接![]()
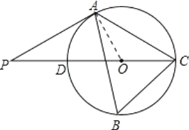
∵∠B=60°
∴∠AOC=2∠B=120°
又∵OA=OC
∴∠OAC=∠OC A=30°
又∵AP=AC
∴∠P=∠ ACP=30°
∴∠OAP=∠A OC-∠P =90°
∴OA⊥PA
∴PA是圆 O 的切线;
(2)解:过点C作CE⊥ AB于点E.
在 Rt△BCE 中,∠B= 60°,
BC =4,
∴![]()
∴![]()
∴在 Rt△ACE 中,![]() ,
,
∴![]()
∴在 Rt△PAO 中,OA=3,
∴⊙O的半径为 3.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数.图象
为常数.图象![]() ,
,![]() 合起来得到的图象记为
合起来得到的图象记为![]() .
.
(1)当![]() 时,
时,
①点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
②求图象![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)当图象![]() 的最低点到
的最低点到![]() 轴距离为
轴距离为![]() 时,求
时,求![]() 的值;
的值;
(3)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,
,![]() ,当图象
,当图象![]() 与线段
与线段![]() 有两个交点时,直接写出
有两个交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,点C1的坐标是_______;
(2)△A1B1C1的面积是_______平方单位.
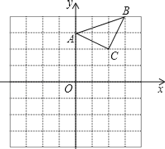
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出五年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.下图是2017年“一年一路”沿线部分国家的通信设施现状统计图.
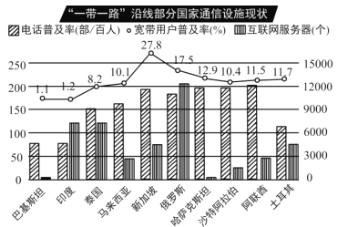
根据统计图提供的信息,下列推断合理的是( ).
A.互联网服务器拥有个数最多的国家是阿联酋
B.宽带用户普及率的中位数是11.05%
C.有8个国家的电话普及率能够达到平均每人1部
D.只有俄罗斯的三项指标均超过了相应的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中 xOy 中,对于⊙C及⊙C内一点 P,给出如下定义:若存在过点 P 的直线 l,使得它与⊙C 相交所截得的弦长为![]() ,则称点 P 为⊙C的“k-近内点”.
,则称点 P 为⊙C的“k-近内点”.
(1)已知⊙O的半径为 4,
①在点中![]() ,⊙O的“4-近内点”是______________;
,⊙O的“4-近内点”是______________;
②点 P 在直线y=![]() x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
(2)⊙C的圆心为(-1,0),半径为 3,直线![]() x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2
x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2![]() -近内点”,则 b 的取值范围是____________.
-近内点”,则 b 的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
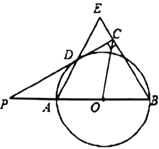
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
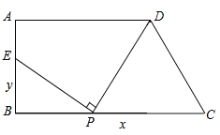
【题目】如图:梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=6,在线段BC上任取一点P,连接DP,作射线PE⊥DP,PE与直线AB交于点E.
(1)试确定当CP=3时,点E的位置;
(2)若设CP=x,BE=y,试写出y关于自变量x的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com