
【题目】已知![]() ,
,![]() 平分
平分![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 、
、![]() 上的动点(
上的动点(![]() 、
、![]() 、
、![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() .
.
(1)如图1,若![]() ,则:
,则:
①![]() 的度数为
的度数为
②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()

(2)如图2,若![]() ,则是否存在这样的
,则是否存在这样的![]() 的值,使得
的值,使得![]() 中有两个想等的角?若存在,求出
中有两个想等的角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

【答案】(1)①24°,②108,54;(2)存在,x=42、24、33、123.
【解析】
(1)①运用平行线的性质以及角平分线的定义,可得①∠ABO的度数;②根据∠ABO、∠BAD的度数以及△AOB的内角和,可得x的值;
(2)分两种情况进行讨论:AC在AB左侧,AC在AB右侧,分别根据三角形内角和定理以及直角的度数,可得x的值.
(1)如图1,
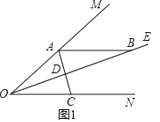
①∵∠MON=48°,OE平分∠MON,
∴∠AOB=∠BON=24°,
∵AB∥ON,
∴∠ABO=24°;
②当∠BAD=∠ABD时,∠BAD=24°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°24°×3=108°;
当∠BAD=∠BDA时,∵∠ABO=24°,
∴∠BAD=78°,∠AOB=24°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°24°24°78°=54°,
故答案为:①24°;②108,54;
(2)如图2,存在这样的x的值,使得△ADB中有两个相等的角.

∵AB⊥OM,∠MON=48°,OE平分∠MON,
∴∠AOB=24°,∠ABO=66°,
①当AC在AB左侧时:
若∠BAD=∠ABD=66°,则∠OAC=90°66°=24°;
若∠BAD=∠BDA=![]() (180°66°)=57°,则∠OAC=90°57°=33°;
(180°66°)=57°,则∠OAC=90°57°=33°;
若∠ADB=∠ABD=66°,则∠BAD=48°,故∠OAC=90°48°=42°;
②当AC在AB右侧时:
∵∠ABE=114°,且三角形的内角和为180°,
∴只有∠BAD=∠BDA=![]() (180°114°)=33°,则∠OAC=90°+33°=123°.
(180°114°)=33°,则∠OAC=90°+33°=123°.
综上所述,当x=24、33、42、123时,△ADB中有两个相等的角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
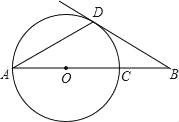
【题目】如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.
(1)求证:BD是⊙O的切线;
(2)求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,在对角线
中,在对角线![]() 上取不同的两点
上取不同的两点![]() (点B、E、F、D依次排列),下列条件中,能得出四边形
(点B、E、F、D依次排列),下列条件中,能得出四边形![]() 一定为平行四边形的是_____________.(A. BE=DF;B. AE=CF C. AE∥CF;D. ∠BAE=∠DCF)
一定为平行四边形的是_____________.(A. BE=DF;B. AE=CF C. AE∥CF;D. ∠BAE=∠DCF)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用代入法解方程组 较简单的解法步骤是:先把方程___变形为__________,再代入方程__________,求得__________的值,然后再求___________的值.
较简单的解法步骤是:先把方程___变形为__________,再代入方程__________,求得__________的值,然后再求___________的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
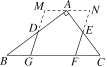
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别是AB,AC的中点,点G,F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地,(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.快车到达甲地时,慢车距离甲地__米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于![]() CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.
CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com