
分析 (1)①根据M{a,b,c}表示这三个数的平均数,进行解答;
②因为用min(a,b,c)表示这三个数中最小的数.分别计算sin60°,cos45°,tan30°的值,因为tan30°最小,所以min{sin60°,cos45°,tan30°}=tan30°;
③由得出2x-5≥3,且-3x+24≥3,两个式子同时成立,据此即可求得x的范围;
(2)①结合题意,分情况讨论,将实际问题与数学思想联系起来,读懂题列出算式即可求解;
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
解答 解:(1)①M{(-2)3,(-3)2,(-$\frac{1}{4}$)-2}=$\frac{(-2)^{3}+(-3)^{2}+(-\frac{1}{4})^{-2}}{3}$=$\frac{17}{3}$,故答案为:$\frac{17}{3}$;
②min{sin60°,cos45°,tan30°}=$\frac{\sqrt{3}}{3}$,故答案为:$\frac{\sqrt{3}}{3}$;
③∵min{3,2x-5,-3x+24}=3,
∴$\left\{\begin{array}{l}{2x-5≥3}\\{-3x+24≥3}\end{array}\right.$
解得:4≤x≤7.
故答案为:4≤x≤7.
(2)①M{2015,x+2014,2x+2013}=$\frac{2015+x+2014+2x+2013}{3}$=x+2014,
∵2x+2013-(x+2014)=x-1.当x≥1时,
则min{2015,x+2014,2x+2013}=2015,则x+2014=2015,
∴x=1.
当x<1时,
则min{2015,x+2014,2x+2013}=2x+2013,则x+2014=2x+2013,
∴x=1(舍去).
综上所述:x=1.
②a=b=c.理由如下:
∵M{a,b,c}=$\frac{a+b+c}{3}$,
如果min{a,b,c}=c,则a≥c,b≥c.
则有$\frac{a+b+c}{3}$=c,即a+b-2c=0,
∴(a-c)+(b-c)=0.
又∵a-c≥0,b-c≥0,
∴a-c=0且b-c=0.
∴a=b=c.
其他情况同理可证,故a=b=c.
故答案为:a=b=c.
(3)由②的结论,若M{3x+y,x+2y+11,4x-y-2}=min{3x+y,x+2y+11,4x-y-2},
则3x+y=x+2y+11=4x-y-2,
解得:x=$-\frac{10}{3}$,y=-$\frac{23}{3}$,
∴x+y=-11.
故答案为:-11.
点评 本题考查了一元一次不等式组的应用,解决的关键是读懂题意,据题意结合方程和不等式去求解,考查综合应用能力.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
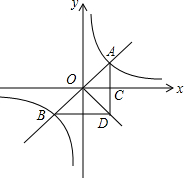 如图,已知直线y=kx与双曲线y=$\frac{k}{x}$相交于A、B两点,过点A作AC垂直于x轴,垂足为C,且S△AOC=$\frac{1}{2}$.过原点O作AB的垂线交AC的延长线于点D,则△ABD的内切圆半径长等于2-$\sqrt{2}$.
如图,已知直线y=kx与双曲线y=$\frac{k}{x}$相交于A、B两点,过点A作AC垂直于x轴,垂足为C,且S△AOC=$\frac{1}{2}$.过原点O作AB的垂线交AC的延长线于点D,则△ABD的内切圆半径长等于2-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
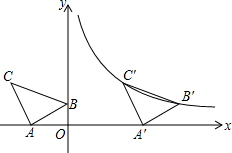 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(d,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(d,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com