
【题目】在抗击新冠肺炎疫情期间,老百姓越来越依赖电商渠道获取必要的生活资料.小石经营的水果店也适时加入了某电商平台,并对销售的水果中的部分(如下表)进行促销:参与促销的水果免配送费且一次购买水果的总价满128元减![]() 元.每笔订单顾客网上支付成功后,小石会得到支付款的80%.
元.每笔订单顾客网上支付成功后,小石会得到支付款的80%.
参与促销水果 | |
水果 | 促销前单价 |
苹果 | 58元/箱 |
耙耙柑 | 70元/箱 |
车厘子 | 100元/箱 |
火龙果 | 48元/箱 |
(1)当![]() 时,某顾客一次购买苹果和车厘子各1箱,需要支付_____元,小石会得到______元;
时,某顾客一次购买苹果和车厘子各1箱,需要支付_____元,小石会得到______元;
(2)在促销活动中,为保障小石每笔订单所得到的金额不低于促销前总价的七折,则![]() 的最大值为_____.
的最大值为_____.
科目:初中数学 来源: 题型:
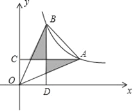
【题目】如图,点A,B为反比例函数y=![]() 在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( )
在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
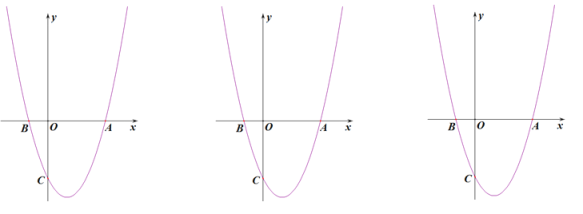
【题目】已知:如图,抛物线y ax2 - 2ax 3a交 x 轴正半轴于点 A,负半轴于点 B,交 y 轴于点C,tan∠OBC=3.
(1)求 a 值;
(2)点 P 为第一象限抛物线上一点,连接 AC、PA、PC,若点 P 的横坐标为 t, PAC 的面积为S,求 S与t的函数解析式,(请直接写出自变量 t 的取值范围);
(3)在(2)的条件下,过点 P 作 PD∥y 轴交 CA 延长线于点 D,连接 PB,交 y 轴于点 E,点 Q 为第二象限抛物线上一点,连接 QE 并延长分别交 x 轴、抛物线于点 N、F,连接 FD,交 x 轴于点 K ,当E 为 QF 的中点且 FN=FK 时,求直线 DF 的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了促进旅游业的发展,要在如图所示的三条公路![]() ,
,![]() ,
,![]() 围成的一块地上修建一个度假村,要使这个度假村到
围成的一块地上修建一个度假村,要使这个度假村到![]() ,
,![]() 两条公路的距离相等,且到
两条公路的距离相等,且到![]() ,
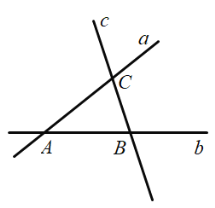
,![]() 两地的距离相等,下列选址方法绘图描述正确的是( )
两地的距离相等,下列选址方法绘图描述正确的是( )
A.画![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,两线的交点符合选址条件
的垂直平分线,两线的交点符合选址条件
B.先画![]() 和
和![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,三线的交点符合选址条件
的垂直平分线,三线的交点符合选址条件
C.画三个角![]() ,
,![]() 和
和![]() 三个角的平分线,交点即为所求
三个角的平分线,交点即为所求
D.画![]() ,
,![]() ,
,![]() 三条线段的垂直平分线,交点即为所求
三条线段的垂直平分线,交点即为所求
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数L:y=mx2+2mx+k(其中m,k是常数,k为正整数).
(1)若L经过点(1,k+6),求m的值.
(2)当m=2,若L与x轴有公共点时且公共点的横坐标为非零的整数,确定k的值;
(3)在(2)的条件下将L:y=mx2+2mx+k的图象向下平移8个单位,得到函数图象M,求M的解析式;
(4)将M的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象N,请结合新的图象解答问题,若直线y=![]() x+b与N有两个公共点时,请直接写出b的取值范围.
x+b与N有两个公共点时,请直接写出b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的一点(不与点
上的一点(不与点![]() 重合),边
重合),边![]() 上点
上点![]() 在点
在点![]() 的右边且
的右边且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
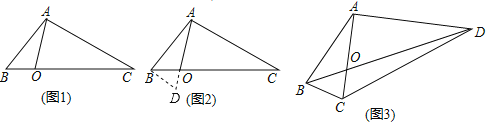
(1)如图1,
①依题意补全图1;
②求证:![]() ;
;
(2)如图2,![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
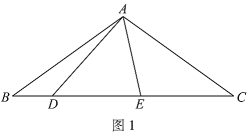
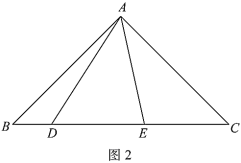
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
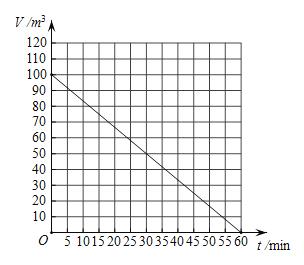
【题目】如图,是用图象反映储油罐内的油量V与输油管开启时间t的函数关系.观察这个图象,以下结论正确的有________________.
①随着输油管开启时间的增加,储油罐内的油量在减少;
②输油管开启10分钟时,储油罐内的油量是80立方米;
③如果储油罐内至少存油40立方米,那么输油管最多可以开启36分钟;
④输油管开启30分钟后,储油罐内的油量只有原油量的一半.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com