
【题目】已知:函数y = (m+1) x+2 m﹣6,
(1)若函数图象过(﹣1 ,2),求此函数的解析式;
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式;
(3)求满足②条件的直线与此同时y =﹣3 x + 1 的交点。
【答案】(1)m=9,y =10x+12;(2)m=1,y =2x-4;(3)交点(1,-2).
【解析】试题分析:(1)根据一次函数图象上点的坐标特征,把(-1,2)代入y=(m+1)x+2m-6求出m的值即可得到一次函数解析式;(2)根据两直线平行的问题得到m+1=2,解出m=1,从而可确定一次函数解析式.(3)两直线的解析式联立方程,解方程即可求得.
试题解析:(1)把(1,2)代入y=(m+1)x+2m6得(m+1)+2m6=2,
解得m=9,
所以一次函数解析式为y=10x+12;
(2)因为函数y=(m+1)x+2m6的图象与直线y=2x+5平行,
所以m+1=2,解得m=1,
所以一次函数解析式为y=2x4.
(3)解![]() 得
得![]() ,
,
∴两直线的交点为(1,2).


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中![]() (分钟)表示所用时间,
(分钟)表示所用时间, ![]() (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
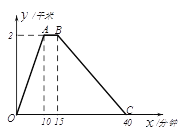
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
查看答案和解析>>
科目:初中数学 来源: 题型:
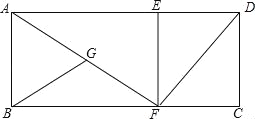
【题目】如图,在矩形ABCD中,AD=25,AB=12,点E、F分别是AD、BC上的点,且DE=CF=9,连接EF、DF、AF.取AF的中点为G,连接BG,将△BFG沿BC方向平移,当点F到达点C时停止平移,然后将△GFB绕C点顺时针旋转α(0°<α<90°),得到△B1CG1(点G的对应点为G1,点B的对应点为B1),在旋转过程中,直线B1G1与直线EF、FD分别相交M、N,当△FMN是等腰三角形,且FM=FN时,线段DN的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com