
我市为改善农村生活条件,满足居民清洁能源的需求,计划为万宝村400户居民修建A、B两种型号的沼气池共24个.政府出资36万元,其余资金从各户筹集.两种沼气池的型号、修建费用、可供使用户数、占地面积如下表:
沼气池 修建费用(万元/个) 可供使用户数(户/个) 占地面积(平方米/个)
A型 3 20 10
B型 2 15 8
政府土地部门只批给该村沼气池用地212平方米,设修建A型沼气池x个,修建两种沼气池共需费用y万元.
(1)求y与x之间函数关系式.
(2)试问有哪几种满足上述要求的修建方案.
(3)要想完成这项工程,每户居民平均至少应筹集多少钱?
科目:初中数学 来源: 题型:
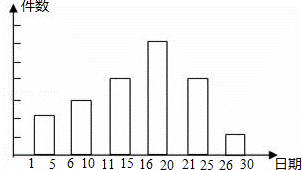
学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.
请你回答:
(1)本次活动共有 件作品参赛;各组作品件数的众数是 件;
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B、D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
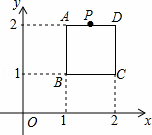
如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
A. 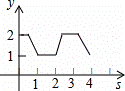 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
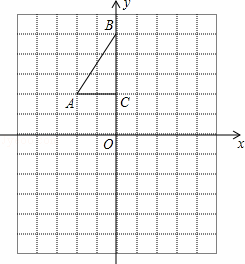
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙三个箱子原本各装有相同数量的球,已知甲箱内的红球占甲箱内球数的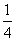 ,
,
乙箱内没有红球,丙箱内的红球占丙箱内球数的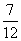 。小蓉将乙、丙两箱内的球全倒入
。小蓉将乙、丙两箱内的球全倒入
甲箱后,要从甲箱内取出一球,若甲箱内每球被取出的机会相等,则小蓉取出的球是红
球的机率为何? (A)  (B)
(B) 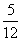 (C)
(C) 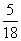 (D)
(D) 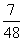
查看答案和解析>>
科目:初中数学 来源: 题型:
小蓁与她的五位朋友参加保龄球比赛,图(十四)为她们六人所得分数的盒状图。若小蓁所得到的分数恰为她们六人的平均分数,则小蓁得到多少分?
(A) 165 (B) 169 (C) 170 (D) 175
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
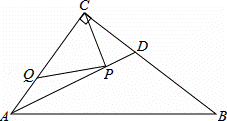
|
| A. |
| B. | 4 | C. |
| D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com