

分析 探究:先在直角△ABH中,由AB=13,cos∠ABC=$\frac{5}{13}$,可得AH=12,BH=5,则CH=9,再解直角△ACH,即可求出AC的值,最后根据三角形的面积公式即可求出S△ABC的值;
拓展:(1)由三角形的面积公式即可求解;
(2)首先由(1)可得m=$\frac{2{S}_{△ABD}}{x}$,n=$\frac{2{S}_{△CBD}}{x}$,再根据S△ABD+S△CBD=S△ABC=84,即可求出(m+n)与x的函数关系式,然后由点D在AC上(可与点A,C重合),可知x的最小值为AC边上的高,最大值为BC的长;
(3)由于BC>BA,所以当以B为圆心,以大于$\frac{56}{5}$且小于13为半径画圆时,与AC有两个交点,不符合题意,故根据点D的唯一性,分两种情况:①当BD为△ABC的边AC上的高时,D点符合题意;②当AB<BD≤BC时,D点符合题意;
发现:由于AC>BC>AB,所以使得A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线.
解答 探究:
解:∵在△ABC中,AB=13,BC=14,cos∠ABC=$\frac{5}{13}$,
∴$\frac{BH}{AB}$=$\frac{5}{13}$,
∴BH=5,
∴AH=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴HC=9,AC=$\sqrt{1{2}^{2}+{9}^{2}}$=15,
∴△ABC的面积S△ABC=$\frac{1}{2}$×12×14=84;
故答案为:12,15,84;
拓展:
解:(1)由三角形面积公式得出:S△ABD=$\frac{1}{2}$mx,S△CBD=$\frac{1}{2}$nx;
(2)∵m=$\frac{2{S}_{△ABD}}{x}$,n=$\frac{2{S}_{△CBD}}{x}$,
∴m+n=$\frac{2{S}_{△ABD}}{x}$+$\frac{2{S}_{△CBD}}{x}$=$\frac{168}{x}$,
∵AC边上的高为:$\frac{2{S}_{△ABC}}{15}$=$\frac{2×84}{15}$=$\frac{56}{5}$,
∴x的取值范围为:$\frac{56}{5}$≤x≤14,
∵(m+n)随x的增大而减小,
∴x=$\frac{56}{5}$时,(m+n)的最大值为:15;
当x=14时,(m+n)的最小值为12;
(3)x的取值范围是x=$\frac{56}{5}$或13<x≤14,
发现:
解:∵AC>BC>AB,
∴过A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线,AC边上的高的长为 $\frac{56}{5}$.
点评 本题是三角形综合题目,考查了解直角三角形,勾股定理,三角形的面积,反比例函数的性质等知识,本题综合性较强,有一定难度.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:选择题
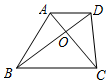 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )| A. | 4:25 | B. | 4:9 | C. | 2:5 | D. | 2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+3y | B. | xy-y=1 | C. | x-3y=5 | D. | $\frac{x}{2}$+$\frac{7}{y}$=$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
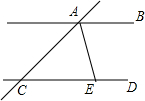 如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )| A. | 40° | B. | 110° | C. | 70° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解2017年春节联欢晚会收视情况 | |
| B. | 为了解全国中学生的视力状况 | |
| C. | 乘坐高铁时,检查旅客行李是否携带有违禁物品 | |
| D. | 为了解2017年春节中国人最喜欢的过年方式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com