
分析 先a+18=c+35得出a-c=17,则可知a,c为一个奇数、一个偶数,由于a,c均为质数,在所有偶数中只有2是质数,即a,c中必有一个数为2,分两种情况计算判断出,再求出b,由此即可得出答案.
解答 解:∵a+18=c+35,
∴a-c=17,
∴a,c为一个奇数、一个偶数,
∵a,c均为质数,在所有偶数中只有2是质数,
∴a=2或c=2,
当a=2时,c=2-17=-15(不合题意舍去);
当c=2时,a=17+2=19,
∵a+18=b+14,
∴b=a+4=19+4=23,
∴b+c-a=23+2-19=6
故答案为:6.
点评 此题是质数与合数,主要考查的是质数及合数的定义,奇数与偶数的定义,解答此类题目的关键是熟知在所有偶数中只有2是质数这一关键的知识点.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
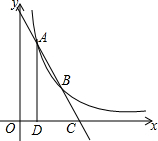 如图,点A(1,4)、B(2,a)在函数y=$\frac{m}{x}$(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
如图,点A(1,4)、B(2,a)在函数y=$\frac{m}{x}$(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A(1,0)、B(4,0)、M(5,3).动点P从A点出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线l:y=-x+b也随之移动.设移动时间为t秒.
如图,点A(1,0)、B(4,0)、M(5,3).动点P从A点出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线l:y=-x+b也随之移动.设移动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com