
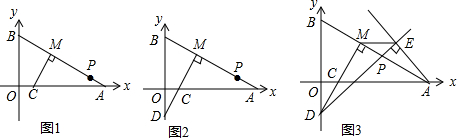
分析 (1)先解方程(m+1)(m+3)-(m+2)(m-2)=15,求得m的值,即可得到M的坐标;
(2)如图①,作辅助线,构建全等三角形,先证明四边形OKMN为正方形得:OK=ON=2,再证明△MNB≌△MKC,则CK=BN,代入OB+OC中可得结论;
(3)如图②,证明△AKM≌△DNM,则S△AKM=S△DNM,所以S△ACM-S△OCD拆成和与差的形式,并等量代换即可;
(4)如图③,作辅助线,构建全等三角形,证明△MDF≌△MAE,得MF=ME,∠DMF=∠AME,再得△FME是等腰直角三角形,即可得出∠DEM=45°.
解答 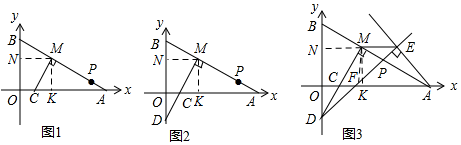 解:(1)∵(m+1)(m+3)-(m+2)(m-2)=15,
解:(1)∵(m+1)(m+3)-(m+2)(m-2)=15,
4m+3+4=15,
∴m=2,
∴M的坐标为(2,2);
(2)如图1,过M作KM⊥x轴,KN⊥y轴,垂足分别为K、N,
则∠MNO=∠MKO=90°,
∵∠BOA=90°,
∴四边形OKMN是矩形,
∴∠NMK=90°,
∴∠NMC+∠CMK=90°,
∵M(2,2),
∴KM=MN=2,
∴矩形OKMN是正方形,
∴OK=ON=2,
∵CM⊥AB,
∴∠BMN+∠NMC=90°,
∴∠BMN=∠CMK,
∵∠MNB=∠CKM=90°,
∴△MNB≌△MKC(ASA),
∴CK=BN,
∴OB+OC=ON+BN+OC=ON+CK+OC=ON+OK=2+2=4;
(3)如图2,∵∠AMC=∠KMN=90°,
∴∠AMK=∠NMD=90°-∠CMK,
∵∠MND=∠MKA=90°,KM=MN,
∴△AKM≌△DNM(ASA),
∴S△AKM=S△DNM,
∴S△ACM-S△OCD=S△AKM+S△CMK-S△OCD
=S△DNM+S△CMK-S△OCD
=S正方形OKMN+S△OCD-S△OCD
=S正方形OKMN
=2×2
=4;
(4)如图3,由(3)得:△AKM≌△DNM,
∴AM=DM,
在DE上截取DF=AE,连接MF,
∵AE⊥EF,DM⊥AB,
∴∠DMP=∠AEP=90°,
∵∠MPD=∠EPA,
∴∠MDF=∠MAE,
∴△MDF≌△MAE(SAS),
∴MF=ME,∠DMF=∠AME,
∵∠DMP=90°,
∴∠DMF+∠FMP=∠AME+∠FMP=∠FME=90°,
∴△FME是等腰直角三角形,
∴∠DEM=45°.
点评 本题是三角形的综合题,考查了全等三角形、正方形、矩形的性质和判定;解决问题的关键是证明三角形全等,利用全等三角形对应边相等和对应角相等得出边与角的关系;同时利用了全等三角形的面积相等,在求解三角形面积的差时,利用三角形面积相等关系进行加减,得出S△ACM-S△OCD的值与正方形的面积相等,从而得出结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 若干个英语字母打乱顺序后排成了如图所示的方阵,若字母L表示为(1,4),则按(3,4),(2,2),(1,3),(4,1)的顺序排列成的英语单词为PARE.
若干个英语字母打乱顺序后排成了如图所示的方阵,若字母L表示为(1,4),则按(3,4),(2,2),(1,3),(4,1)的顺序排列成的英语单词为PARE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
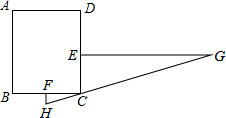 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长 9 里,城墙BC长 7 里,东门所在的点E,南门所在的点F分别是CD,BC 的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=1.05里.
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长 9 里,城墙BC长 7 里,东门所在的点E,南门所在的点F分别是CD,BC 的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=1.05里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
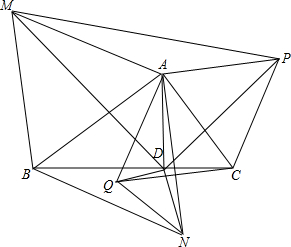 AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.
AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
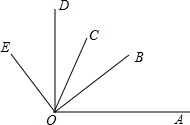 如图,OB是∠AOC的平分线,OD是∠COE的平分线.
如图,OB是∠AOC的平分线,OD是∠COE的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com