
����Ŀ������֪�������������Ĺ��̳�Ϊ֤����֤���ij�����������ǻ�����ʵ.֤��������ȫ�ȵĻ�����ʵ�У�������нǷֱ���ȵ�����������ȫ�ȣ����Ǽ���б߷ֱ���ȵ�����������ȫ�ȣ����߷ֱ���ȵ�����������ȫ��.
��1����ѡ���������ϻ�����ʵ���������ڽǺͶ������������ͼ�Σ�֤�������Ƿֱ����������һ��ȽǵĶԱ���ȵ�����������ȫ��.

��2���������ε������ߺ�������ͳ��Ϊ�����ε�����Ԫ��.����������������ĶԶ�ӦԪ����ȣ�������������һ��ȫ������˵������.
���𰸡���1��֤������⣻��2������������һ��ȫ�ȣ����ɼ����.
��������
��1��ͨ��������Ⱥ��������ڽǺͶ�����֪��������Ҳ��ȣ�Ȼ���������Ǽ��б߷ֱ���ȼ���֤����������ȫ�ȣ�
��2���ĶԶ�ӦԪ����ȣ��ɷ��������: ���������ߺ���һ�Ƕ�Ӧ��ȣ����������ߺ������Ƕ�Ӧ��ȣ� ���������Ǻ���һ�߶�Ӧ��ȣ�������������ۼ���.
��1����֪��![]() ֤����
֤����![]()
֤������![]() ��
��![]()
�֡�![]()
��![]()
��![]() ��
��![]() ��
�У�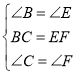
��![]()
��2������������һ��ȫ�ȣ��������£�
������������ߺ���һ�Ƕ�Ӧ��ȣ�����SSS֤����������ȫ�ȣ�
������������ߺ������Ƕ�Ӧ��ȣ������ASA��SAS֤����������ȫ�ȣ�
������������Ǻ���һ�߶�Ӧ��ȣ�����ASA֤����������ȫ��.
�����������������ĶԶ�ӦԪ����ȣ�������������һ��ȫ��.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� Rt��ABC �У���BAC=90����AB=6,AC=8,D Ϊ AC ��һ�㣬����ABD �� BD �۵���ʹ�� A ǡ������ BC �ϵ� E �������ۺ� BD �ij��ǣ� ��

A.5B.![]() C.3
C.3 ![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ���֪����ͼ��1���������ΪS����ABC�У� BC=a,AC=b, AB=c,����ԲO�İ뾶Ϊr����OA��OB��OC����ABC������Ϊ����С�����Σ�
![]()
��![]() ��
��

��1����������������ΪS���ı���ABCD��������Բ������߶����е�Բ������ͼ��2�������߳��ֱ�ΪAB=a��BC=b��CD=c��AD=d�����ı��ε�����Բ�뾶r��
��2������Ӧ�ã���ͼ(3)���ڵ�������ABCD�У�AB��DC��AB=21��CD=11��AD=13����O1���O2�ֱ�Ϊ��ABD���BCD������Բ�������ǵİ뾶�ֱ�Ϊr1��r2����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����ͼ��ʾ�Ķ��κ���y=ax2+bx+c��a��0����ͼ���У��۲�ó�������������Ϣ����b2��4ac��0����c��1����ab��0����a��b+c��0������Ϊ������ȷ���У� ����

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪x1��3�ǹ���x��һԪ���η���x2��4x��c��0��һ��������c��ֵ�ͷ��̵���һ����.
��2����ͼ���ھ���ABCD�У���O�ڱ�AB�ϣ���AOC=��BOD����֤��AO=OB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90������б��AB��һ��OΪԲ�ģ�OBΪ�뾶����O����AC�ڵ�E����AB�ڵ�D���ҡ�BEC=��BDE��

��1����֤��AC�ǡ�O�����ߣ�
��2������OC��BE�ڵ�F����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣�ijУ�ڻ��زμ����ʵ�������У�������ʦ����ѧ�������ؼƻ��½�һ�����ε������أ�һ�߿���ǽ��ǽ�㹻�����������������ܳ�69�IJ����դ��Χ�ɣ���ǽƽ�е�һ����һ����Ϊ3�ij���ڣ���ͼ��ʾ�������Ʋ���ʹ�صĶ��������������λѧ��������龳��
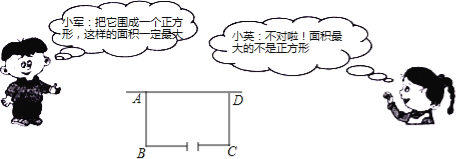
������������Ϣ��������⣺
��1����AB=x�ף�x��0�������ú�x�Ĵ���ʽ��ʾBC�ij���
��2�������ж�˭��˵����ȷ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬��֪B������Ϊ��4��0����
��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬��֪B������Ϊ��4��0����
��1���������ߵĽ���ʽ��
��2����̽����ABC�����Բ��Բ��λ�ã������Բ�����ꣻ
��3������M���߶�BC�·�����������һ�㣬����MBC����������ֵ���������ʱM������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90������B��30������AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��������˵������ȷ�ĸ����ǣ�������
MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��������˵������ȷ�ĸ����ǣ�������
��AD�ǡ�BAC��ƽ���ߣ��ڡ�ADC��60�����۵�D��AB���д����ϣ�

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com