
【题目】如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
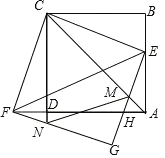
(1)证明:点A、D、F在同一条直线上;
(2)随着点E的移动,线段DH是否有最小值?若有,求出最小值;若没有,请说明理由;
(3)连结EF、MN,当MN∥EF时,求AE的长.
【答案】(1)见解析;(2)有最小值,DH的最小值为![]() ;(3)AE= 2
;(3)AE= 2![]() .
.
【解析】
(1)要证明点A、D、F在同一条直线上,只需证明∠CDF+∠CDA=180°即可.根据题中的已知条件很容易证明△DCF≌△BCE,则∠CDF=∠B=90°,结论可证.
(2)设AE=x,DH=y,通过已知条件证明△ECB∽△HEA,利用相似三角形的性质可知![]() ,即可得到一个y与x的二次函数,根据二次函数的最值可求出线段DH的最小值.
,即可得到一个y与x的二次函数,根据二次函数的最值可求出线段DH的最小值.
(3)利用矩形的性质及平行线的性质可证明△CFN≌△CEM,进而推出∠FCN=∠ECM=∠BCE=22.5°. 在BC上取一点K,使得KC=KE,则△BKE是等腰直角三角形,设BE=BK=a,则KC=KE=![]() a,利用
a,利用![]() 求出a的值,从而利用
求出a的值,从而利用![]() 即可求AE的长.
即可求AE的长.
(1)证明:∵四边形ABCD是正方形,
∴CD=CB,∠BCD=∠B=∠ADC=90°,
∵CE=CF,∠ECF=90°,
∴∠ECF=∠DCB,
∴∠DCF=∠BCE,
∴△DCF≌△BCE,
∴∠CDF=∠B=90°,
∴∠CDF+∠CDA=180°,
∴点A、D、F在同一条直线上.
(2)解:有最小值.
理由:设AE=x,DH=y,则AH=1-y,BE=1-x,
∵四边形CFGE是矩形,
∴∠CEG=90°,
∴∠CEB+∠AEH=90°
CEB+∠ECB=90°,
∴∠ECB=∠AEH,
∵∠B=∠EAH=90°,
∴△ECB∽△HEA,
![]()
即![]()
![]()
∵a=1>0,
∴当![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() ,
,
∴DH的最小值为![]() .
.
(3)解:∵四边形CFGE是矩形,CF=CE,
∴四边形CFGE是正方形,
∴GF=GE,∠GFE=∠GEF=45°,
∵NM∥EF,
∴∠GNM=∠GFE,∠GMN=∠GEF,
∴∠GMN=∠GNM,
∴GN=GM,
∴FN=EM,
∵CF=CE,∠CFN=∠CEM,
∴△CFN≌△CEM,
∴∠FCN=∠ECM,
∵∠MCN=45°,
∴∠FCN=∠ECM=∠BCE=22.5°,
在BC上取一点K,使得KC=KE
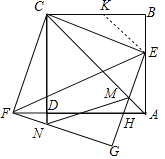
![]()
![]()
![]()
∴△BKE是等腰直角三角形
设BE=BK=a,则KC=KE=![]() a,
a,
![]()
![]()
![]()


科目:初中数学 来源: 题型:
【题目】张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
步行数(步) | 10672 | 4927 | 5543 | 6648 | ||
步行距离(公里) | 6.8 | 3.1 | 3.4 | 4.3 | ||
卡路里消耗(千卡) | 157 | 79 | 91 | 127 | ||
燃烧脂肪(克) | 20 | 10 | 12 | 16 |
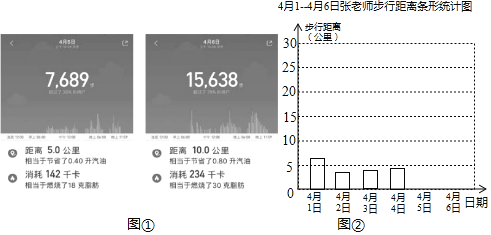
(1)请你将手环记录的4月5日和4月6日的数据(如图①)填入表格
(2)请你将条形统计图(如图②)补充完整
(3)张老师这6天平均每天步行约______公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为______公里(精确到0.1公里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)该公司营销员销售该品牌电脑的月销售平均数是 台,中位数是 台,众数是 台.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
![]() ______,
______,![]() ______.
______.
![]() 该调查统计数据的中位数是______,众数是______.
该调查统计数据的中位数是______,众数是______.
![]() 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
![]() 若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连结AB.
(1)求证:AB2=AE·AD;
(2)若AE=2,ED=4,求图中阴影的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 和点
和点![]() .
.

(1)求直线![]() 与反比例函数的解析式;
与反比例函数的解析式;
(2)求![]() 的度数;
的度数;
(3)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角(
角(![]() 为锐角),得到
为锐角),得到![]() ,当
,当![]() 为多少度时
为多少度时![]() ,并求此时线段
,并求此时线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 经过原点
经过原点![]() ,
,![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)如图2,点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图3,在(2)的条件下,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,作
,作![]() ,连接
,连接![]() 交抛物线于点
交抛物线于点![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com