
分析 运用了一次函数,反比例函数,二次函数的增减性,需要根据这些函数的性质及自变量的取值范围,逐一判断.
解答 解:①y=-$\frac{1}{2}$x是正比例函数,k=-$\frac{1}{2}$<0,y随x的增大而减小;
②y=2x-1是一次函数,k=2>0,y随着x的增大而增大正确;
③y=$\frac{4}{x}$(x>0)是反比例函数,k>0,在每个象限内y随x的增大而减小;
④y=-$\frac{2}{x}$反比例函数,在每一个象限内,y随着x的增大而增大,故错误;
⑤⑥均为反比例函数,且k<0,在各自的自变量的取值范围内y随x的增大而增大,正确.
故答案为②⑤⑥.
点评 主要考查了一次函数,正比例函数,反比例函数的基本性质,这些性质要掌握才能灵活运用.


科目:初中数学 来源: 题型:解答题
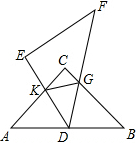 如图.将两块完全一样的透明等腰直角角形板ABC、DEF按如图所示的方式放置,使点D落在线段AB的中点处,直角边DE与直角边AC相交于点K,斜边DF与直角边相交于点G,连接KG.
如图.将两块完全一样的透明等腰直角角形板ABC、DEF按如图所示的方式放置,使点D落在线段AB的中点处,直角边DE与直角边AC相交于点K,斜边DF与直角边相交于点G,连接KG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
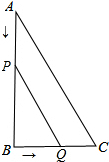 如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发.
如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com