
【题目】如图,在等腰△ABC中,底边BC=12cm,高AD=8cm,四边形PQRS是正方形.
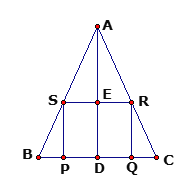
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组为解决当地贫困问题,带领大家致富.经过调查研究,他们决定利用当地生产的甲乙两种原料开发A,B两种商品,为科学决策,他们试生产A、B两种商品100千克进行深入研究,已知现有甲种原料293千克,乙种原料314千克,生产1千克A商品,1千克B商品所需要的甲、乙两种原料及生产成本如下表所示.
甲种原料(单位:千克) | 乙种原料(单位:千克) | 生产成本(单位:元) | |
A商品 | 3 | 2 | 120 |
B商品 | 2.5 | 3.5 | 200 |
设生产A种商品x千克,生产A、B两种商品共100千克的总成本为y元,根据上述信息,解答下列问题:
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)x取何值时,总成本y最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 , ![]() 中,
中, ![]() ,线段
,线段![]() 在射线
在射线![]() 上,且
上,且![]() ,线段
,线段![]() 沿射线
沿射线![]() 运动,开始时,点
运动,开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动停止,过点
时运动停止,过点![]() 作
作![]() ,与射线
,与射线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 相交于点
相交于点![]() .设
.设![]() ,四边形
,四边形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 关于
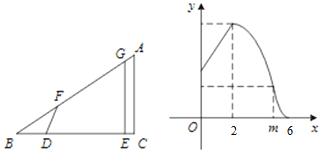
关于![]() 的函数图象如图所示(其中
的函数图象如图所示(其中![]() 时,函数的解析式不同)
时,函数的解析式不同)
(1)填空: ![]() 的长是 ;
的长是 ;
(2)求![]() 关于
关于![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示1,现将点
表示1,现将点![]() 沿数轴作如下移动,第一次点
沿数轴作如下移动,第一次点![]() 向左移动2个单位长度到达点
向左移动2个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动4个单位长度到达点
向右移动4个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动6个单位长度到达点
向左移动6个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离是21,那么
与原点的距离是21,那么![]() 的值是________________.
的值是________________.
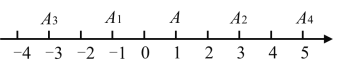
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的水上乐园有一批![]() 人座的自划船,每艘可供
人座的自划船,每艘可供![]() 至
至![]() 位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加.水上乐园的工作人员在去年
位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加.水上乐园的工作人员在去年![]() 月
月![]() 日一天出租的
日一天出租的![]() 艘次
艘次![]() 人自划船中随机抽取了
人自划船中随机抽取了![]() 艘,对其中抽取的每艘船的乘坐人数进行统计,并制成如下统计图.
艘,对其中抽取的每艘船的乘坐人数进行统计,并制成如下统计图.
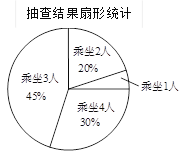
(1)求扇形统计图中, “乘坐1人”所对应的圆心角度数;
(2)估计去年![]() 月
月![]() 日这天出租的
日这天出租的![]() 艘次
艘次![]() 人自划船平均每艘船的乘坐人数;
人自划船平均每艘船的乘坐人数;
(3)据旅游局预报今年![]() 月
月![]() 日这天该景区可能将增加游客300人,请你为景区预计这天需安排多少艘4人座的自划船才能满足需求.
日这天该景区可能将增加游客300人,请你为景区预计这天需安排多少艘4人座的自划船才能满足需求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com