
 +b½»ÕŪĻßO-A-BÓŚµćE£®
+b½»ÕŪĻßO-A-BÓŚµćE£®
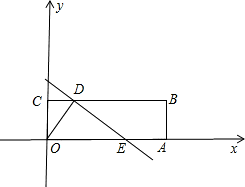 ½ā£ŗ£Ø1£©”ß¾ŲŠĪOABCÖŠ£¬µćA£¬CµÄ×ų±ź·Ö±šĪŖ£Ø6£¬0£©£¬£Ø0£¬2£©£¬
½ā£ŗ£Ø1£©”ß¾ŲŠĪOABCÖŠ£¬µćA£¬CµÄ×ų±ź·Ö±šĪŖ£Ø6£¬0£©£¬£Ø0£¬2£©£¬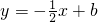 ¾¹żµćC£Ø0£¬2£©£¬Ōņb=2£»
¾¹żµćC£Ø0£¬2£©£¬Ōņb=2£»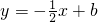 ¾¹żµćA£Ø6£¬0£©£¬Ōņb=3£»
¾¹żµćA£Ø6£¬0£©£¬Ōņb=3£»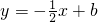 ¾¹żµćB£Ø6£¬2£©£¬Ōņb=5£®
¾¹żµćB£Ø6£¬2£©£¬Ōņb=5£®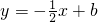 ÉĻ£¬
ÉĻ£¬ £®
£® ÉĻ
ÉĻ
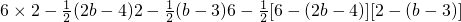 =-b2+5b£®
=-b2+5b£®
 x+b
x+b =
=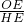 £¬
£¬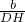 =
= £¬
£¬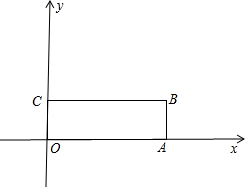 £Ø1£©ŅņĪŖĖıߊĪOABCŹĒ¾ŲŠĪ£¬µćA£¬CµÄ×ų±ź·Ö±šĪŖ£Ø6£¬0£©£¬£Ø0£¬2£©£¬¼“æÉĒó³öµćBµÄ×ų±ź£¬°ŃA”¢B”¢CµÄ×ų±ź“śČė½āĪöŹ½Ēó³öb£¬¼“æÉĒó³ö“š°ø£»
£Ø1£©ŅņĪŖĖıߊĪOABCŹĒ¾ŲŠĪ£¬µćA£¬CµÄ×ų±ź·Ö±šĪŖ£Ø6£¬0£©£¬£Ø0£¬2£©£¬¼“æÉĒó³öµćBµÄ×ų±ź£¬°ŃA”¢B”¢CµÄ×ų±ź“śČė½āĪöŹ½Ēó³öb£¬¼“æÉĒó³ö“š°ø£»

 ³¤½×÷Ņµ±¾Ķ¬²½Į·Ļ°²įĻµĮŠ“š°ø
³¤½×÷Ņµ±¾Ķ¬²½Į·Ļ°²įĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±y=
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±y=| 3 |
| 2 |
| 16 |
| x |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŌµćO“¦ÓŠŅ»Ę¹ÅŅĒņ·¢ÉäĘ÷ĻņæÕÖŠ·¢ÉäĘ¹ÅŅĒņ£¬Ę¹ÅŅĒņ·ÉŠŠĀ·ĻߏĒŅ»ĢõÅ×ĪļĻߣ¬ŌŚµŲĆęÉĻĀäµćĀäŌŚXÖįÉĻĪŖµćB£®ÓŠČĖŌŚĻ߶ĪOBÉĻµćC£ØææµćBŅ»²ą£©ŹśÖ±ĻņÉĻ°Ś·ÅĪŽøĒµÄŌ²ÖłŠĪĶ°£¬ŹŌĶ¼ČĆĘ¹ÅŅĒņĀäČėĶ°ÄŚ£®ŅŃÖŖOB=4Ć×£¬OC=3Ć×£¬Ę¹ÅŅĒņ·ÉŠŠ×ī“óø߶ČMN=5Ć×£¬Ō²ÖłŠĪĶ°µÄÖ±¾¶ĪŖ0.5£¬øßĪŖ0.3Ć×£ØĘ¹ÅŅĒņµÄĢå»żŗĶŌ²ÖłŠĪĶ°µÄŗń¶ČŗöĀŌ²»¼Ę£©£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŌµćO“¦ÓŠŅ»Ę¹ÅŅĒņ·¢ÉäĘ÷ĻņæÕÖŠ·¢ÉäĘ¹ÅŅĒņ£¬Ę¹ÅŅĒņ·ÉŠŠĀ·ĻߏĒŅ»ĢõÅ×ĪļĻߣ¬ŌŚµŲĆęÉĻĀäµćĀäŌŚXÖįÉĻĪŖµćB£®ÓŠČĖŌŚĻ߶ĪOBÉĻµćC£ØææµćBŅ»²ą£©ŹśÖ±ĻņÉĻ°Ś·ÅĪŽøĒµÄŌ²ÖłŠĪĶ°£¬ŹŌĶ¼ČĆĘ¹ÅŅĒņĀäČėĶ°ÄŚ£®ŅŃÖŖOB=4Ć×£¬OC=3Ć×£¬Ę¹ÅŅĒņ·ÉŠŠ×ī“óø߶ČMN=5Ć×£¬Ō²ÖłŠĪĶ°µÄÖ±¾¶ĪŖ0.5£¬øßĪŖ0.3Ć×£ØĘ¹ÅŅĒņµÄĢå»żŗĶŌ²ÖłŠĪĶ°µÄŗń¶ČŗöĀŌ²»¼Ę£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 1 | 3 |

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 Ļą½»ÓŚµćC£®
Ļą½»ÓŚµćC£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŌµćO“¦ÓŠŅ»Ę¹ÅŅĒņ·¢ÉäĘ÷ĻņæÕÖŠ·¢ÉäĘ¹ÅŅĒņ£¬Ę¹ÅŅĒņ·ÉŠŠĀ·ĻߏĒŅ»ĢõÅ×ĪļĻߣ¬ŌŚµŲĆęÉĻĀäµćĀäŌŚXÖįÉĻĪŖµćB£®ÓŠČĖŌŚĻ߶ĪOBÉĻµćC£ØææµćBŅ»²ą£©ŹśÖ±ĻņÉĻ°Ś·ÅĪŽøĒµÄŌ²ÖłŠĪĶ°£¬ŹŌĶ¼ČĆĘ¹ÅŅĒņĀäČėĶ°ÄŚ£®ŅŃÖŖOB=4Ć×£¬OC=3Ć×£¬Ę¹ÅŅĒņ·ÉŠŠ×ī“óø߶ČMN=5Ć×£¬Ō²ÖłŠĪĶ°µÄÖ±¾¶ĪŖ0.5£¬øßĪŖ0.3Ć×£ØĘ¹ÅŅĒņµÄĢå»żŗĶŌ²ÖłŠĪĶ°µÄŗń¶ČŗöĀŌ²»¼Ę£©£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŌµćO“¦ÓŠŅ»Ę¹ÅŅĒņ·¢ÉäĘ÷ĻņæÕÖŠ·¢ÉäĘ¹ÅŅĒņ£¬Ę¹ÅŅĒņ·ÉŠŠĀ·ĻߏĒŅ»ĢõÅ×ĪļĻߣ¬ŌŚµŲĆęÉĻĀäµćĀäŌŚXÖįÉĻĪŖµćB£®ÓŠČĖŌŚĻ߶ĪOBÉĻµćC£ØææµćBŅ»²ą£©ŹśÖ±ĻņÉĻ°Ś·ÅĪŽøĒµÄŌ²ÖłŠĪĶ°£¬ŹŌĶ¼ČĆĘ¹ÅŅĒņĀäČėĶ°ÄŚ£®ŅŃÖŖOB=4Ć×£¬OC=3Ć×£¬Ę¹ÅŅĒņ·ÉŠŠ×ī“óø߶ČMN=5Ć×£¬Ō²ÖłŠĪĶ°µÄÖ±¾¶ĪŖ0.5£¬øßĪŖ0.3Ć×£ØĘ¹ÅŅĒņµÄĢå»żŗĶŌ²ÖłŠĪĶ°µÄŗń¶ČŗöĀŌ²»¼Ę£©£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com