
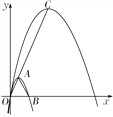
【题目】如图,抛物线C1:y=-![]() x2+2
x2+2![]() x的顶点为A,与x轴的正半轴交于点B.
x的顶点为A,与x轴的正半轴交于点B.
(1)将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的表达式;
(2)将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2,抛物线C2的顶点为C,求抛物线C2的表达式(用k表示);
(3)在(2)条件下,点P在抛物线C2上,满足S△PAC=S△ABC,且∠ACP=90°.当k>1时,求k的值.
【答案】(1)y=-![]() x2+2
x2+2![]() x;(2) y=-
x;(2) y=-![]() x2+2
x2+2![]() x;(3) k=
x;(3) k=![]()
【解析】(1)由抛物线C1解析式求出A、B及原点坐标,将三点坐标都扩大到原来的2倍,利用待定系数法求解可得;
(2)与(1)同理,利用待定系数法可得抛物线C2的解析式;
(3)求出顶点C的坐标,根据 S△PAC=S△ABC知BP∥AC,继而可得△ABO是边长为2的正三角形,四边形CEBP是矩形,表示出点P的坐标,将其代入到抛物线C2解析式可求得k的值.
解:(1)∵y=-![]() x2+2
x2+2![]() x=-
x=-![]() (x-1)2+
(x-1)2+![]() ,
,
∴抛物线C1经过原点O,点A(1,![]() )和点B(2,0)三点,
)和点B(2,0)三点,
∵将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,
∴变换后的抛物线经过原点O,(2,2![]() )和(4,0)三点.
)和(4,0)三点.
设变换后抛物线的表达式为y=ax2+bx,将(2,2![]() )和(4,0)代入,
)和(4,0)代入,
得![]() ,解得
,解得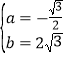 .
.
∴变换后抛物线的表达式为y=-![]() x2+2
x2+2![]() x;
x;
(2)∵抛物线C1经过原点O,点A(1,![]() )和点B(2,0)三点,
)和点B(2,0)三点,
将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2,则抛物线C2过原点O,(k,![]() k),(2k,0)三点,
k),(2k,0)三点,
∴抛物线C2的表达式为y=-![]() x2+2
x2+2![]() x;
x;
(3)∵y=-![]() x2+2
x2+2![]() x=-
x=-![]() (x-k)2+
(x-k)2+![]() k,
k,
∴O,A,C三点共线,且顶点C为(k,![]() k).
k).
如答图,∵S△PAC=S△ABC,k>1,∴BP∥AC,
过点P作PD⊥x轴于D,过点B作BE⊥AO于E.
由题意知△ABO是边长为2的正三角形,四边形CEBP是矩形,
∴OE=1,CE=BP=2k-1,∵∠PBD=60°,
∴BD=k-![]() ,PD=
,PD=![]() (2k-1),
(2k-1),
∴P![]() ,
,
∴![]() (2k-1)=-
(2k-1)=-![]() ,解得k=
,解得k=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
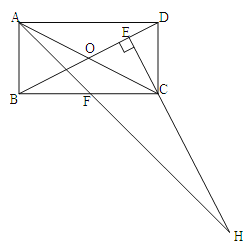
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE![]() BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校美术组要去商店购买铅笔和橡皮,若购买60支铅笔和30块橡皮,则需按零售价购买,共支付30元;若购买90支铅笔和60块橡皮,则可按批发价购买,共支付40.5元.已知每支铅笔的批发价比零售价低0.05元,每块橡皮的批发价比零售价低0.10元.
(1)求每支铅笔和每块橡皮的批发价各是多少元?
(2)小亮同学用4元钱在这家商店按零售价买同样的铅笔和橡皮(两样都要买,4元钱恰好用完),共有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点p第2019次碰到矩形的边时点P的坐标为( )

A. ( 1,4 )B. ( 5,0 )C. ( 8,3 )D. ( 6,4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
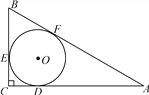
【题目】如图,⊙O为△ABC的内切圆,切点分别为D,E,F,∠C=90°,BC=3,AC=4.
(1)求△ABC的面积;
(2)求⊙O的半径;
(3)求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com