
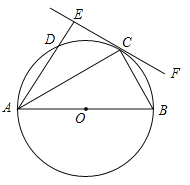
【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧![]() 的长l.
的长l.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据等腰三角形的性质得到∠OAC=∠DAC,求得∠DAC=∠OCA,推出AD∥OC,得到∠OCF=∠AEC=90°,于是得到结论;
(2)连接OD,DC,根据角平分线的定义得到∠DAC=∠OAC,根据三角函数的定义得到∠ECD=30°,得到∠OCD=60°,得到∠BOC=∠COD=60°,OC=2,于是得到结论.
试题解析:(1)证明:连接OC,∵OA=OC,∴∠OAC=∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∵∠AEC=90°,∴∠OCF=∠AEC=90°,∴EF是⊙O的切线;
(2)连接OD,DC,∵∠DAC=![]() ∠DOC,∠OAC=
∠DOC,∠OAC=![]() ∠BOC,∴∠DAC=∠OAC,∵ED=1,DC=2,∴sin∠ECD=
∠BOC,∴∠DAC=∠OAC,∵ED=1,DC=2,∴sin∠ECD=![]() ,∴∠ECD=30°,∴∠OCD=60°,∵OC=OD,∴△DOC是等边三角形,∴∠BOC=∠COD=60°,OC=2,∴l=
,∴∠ECD=30°,∴∠OCD=60°,∵OC=OD,∴△DOC是等边三角形,∴∠BOC=∠COD=60°,OC=2,∴l=![]() =
=![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
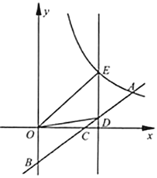
(1)![]() ________,点
________,点![]() 的坐标为________;
的坐标为________;
(2)若点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴,交反比例函数图像于点
轴,交反比例函数图像于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品,新冠疫情期间,为了减少库存,甲、乙两家商场打折促销,甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
⑴.以![]() (单位:元)表示商品原价,
(单位:元)表示商品原价,![]() (单位:元)表示实际购物金额,分别就两家商场的让利方式写出
(单位:元)表示实际购物金额,分别就两家商场的让利方式写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
⑵.新冠疫情期间如何选择这两家商场去购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
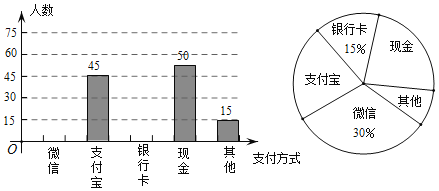
【题目】随着科技的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份“你最喜欢的支付方式”调查问卷(每人必选且只选一种),在某商场随机调查了部分顾客,并将统计结果绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人,在扇形统计图中,表示“现金”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是 ;
(3)运用这次的调查结果估计1000名顾客中用“支付宝”支付的有多少人?
(4)在一次购物中,嘉嘉和琪琪都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
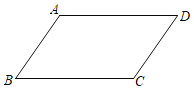
【题目】如图,在ABCD中,已知AD>AB.且AB=5.
(1)作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(保留作图痕迹,不写作法)
(2)若四边形ABEF的周长为a,求a的值
(3)根据(2),先化简W=(a+2)2﹣(a2+1),再求W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C

(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
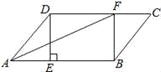
【题目】如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com