
【题目】如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )
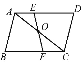
A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】
由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,可根据上述特点对各结论进行判断.
△ABC与△CDA关于点O对称,则AB=CD、AD=BC,所以四边形ABCD是平行四边形,
因此点O就是ABCD的对称中心,则有:
(1)点E和点F;B和D是关于中心O的对称点,正确;
(2)直线BD必经过点O,正确;
(3)四边形ABCD是中心对称图形,正确;
(4)四边形DEOC与四边形BFOA的面积必相等,正确;
(5)△AOE与△COF成中心对称,正确;
其中正确的个数为5个,
故选D.


科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划用![]() 元从厂家购进
元从厂家购进![]() 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入![]() 台,其中每台的价格、销售获利如下表:
台,其中每台的价格、销售获利如下表:
甲型 | 乙型 | 丙型 | |
价格(元/台) |
|
|
|
销售获利(元/台) |
|
|
|
![]() 购买丙型设备 台(用含
购买丙型设备 台(用含![]() 的代数式表示) ;
的代数式表示) ;
![]() 若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了![]() 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?
![]() 在第
在第![]() 题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE
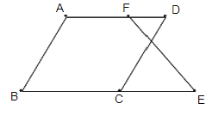
证明:∵∠B+∠BCD=180°(已知)
∴AB∥CD( )
∴∠B=∠DCE( )
又∵∠B=∠D(已知 ),
∴___________ (等量代换)
∴ ∥
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
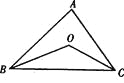
【题目】如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
例如:分解因式![]() ;求代数式
;求代数式![]() 的最小值,
的最小值,![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _______.
_______.
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最大值?并求出这个最大值.
有最大值?并求出这个最大值.
(3)利用配方法,尝试解方程![]() ,并求出
,并求出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com