
分析 根据垂径定理和特殊角的三角函数值,分两种情况计算即可.
解答 解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.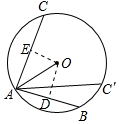
∵OE⊥AC,OD⊥AB,根据垂径定理得AE=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$,AD=$\frac{1}{2}$AB=$\frac{\sqrt{2}}{2}$,
∴sin∠AOE=$\frac{AE}{AO}$=$\frac{\sqrt{3}}{2}$,sin∠AOD=$\frac{AD}{AO}$=$\frac{\sqrt{2}}{2}$,
根据特殊角的三角函数值可得∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°-60°=30°,
∴∠BAC=45°+30°=75°,
或∠BAC′=45°-30°=15°.
15°或75°.
点评 此题主要考查了垂径定理和勾股定理,灵活运用相关定理是解题的关键,注意要考虑到两种情况.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…,An,….将抛物线y=x2沿直线L:y=$\frac{1}{2}$x平移得一系列抛物线,且同时满足下列两个条件:
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…,An,….将抛物线y=x2沿直线L:y=$\frac{1}{2}$x平移得一系列抛物线,且同时满足下列两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y1<y2 | D. | y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com