
【题目】某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与《新型冠状病毒防治与预防知识》作答(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行数据统计、数据分析.
甲 | 85 | 80 | 95 | 85 | 90 | 95 | 100 | 65 | 75 | 85 |
90 | 90 | 70 | 100 | 90 | 80 | 80 | 90 | 98 | 75 | |
乙 | 80 | 60 | 80 | 85 | 95 | 65 | 90 | 85 | 100 | 80 |
95 | 75 | 80 | 80 | 70 | 100 | 95 | 75 | 90 | 90 |
表1分数统计表
成绩 小区 | 60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 |
甲 | 2 | 5 | a | b |
乙 | 3 | 7 | 5 | 5 |
表2:频数分布表
统计量 小区 | 平均数 | 中位数 | 众数 |
甲 | 85.75 | 87.5 | c |
乙 | 83.5 | d | 80 |
表3:统计量
(1)填空:a= ,b= ,c= ,d= ;
(2)甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)对于此次抽样调查中测试成绩为60≤x≤70的居民,社区鼓励他们重新学习,然后从中随机抽取两名居民进行测试,求刚好抽到一个是甲小区居民,另一个是乙小区居民的概率.
【答案】(1)8,5,90,82.5;(2)200人.(3)![]()
【解析】
(1)数出甲小区80<x≤90的数据数可求a;甲小区90<x≤100的数据数可求b;根据中位数的意义,将乙小区的抽查的20人成绩排序找出处在中间位置的两个数的平均数即可为中位数,从甲小区成绩中找出出现次数最多的数即为众数;
(2)抽查甲小区20人中成绩高于90分的人数有5人,因此甲小区成绩大于90分的人数占抽查人数为25%,进而可估计甲小区成绩大于90分的人数;
(3)列举出所有等可能结果,利用概率公式求解可得.
(1)数出甲小区80<x≤90的数据数得到:![]() ,
,
数出甲小区90<x≤100的数据数得到:![]() ,
,
甲小区的出现次数最多的是90,因此众数是90,即c=90,
中位数是从小到大排列后处在第10、11位两个数的平均数,
由乙小区中的数据可得处在第10、11位的两个数的平均数为(80+85)÷2=82.5,
因此d=82.5.
故答案为:8,5,90,82.5;
(2)800×![]() =200(人).
=200(人).
答:估计甲小区成绩大于90分的人数是200人.
(3)设乙小区三个人编号为A、B、C,甲小区编号为D、E,
则所有可能组合为:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10种,其中刚好抽到一个是甲小区居民,另一个是乙小区居民的情况数为6种,
∴刚好抽到一个是甲小区居民,另一个是乙小区居民的概率=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
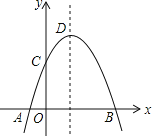
【题目】如图,抛物线y=﹣x2+2x+c+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①抛物线的对称轴是直线x=1;
②若OC=OB,则c=2;
③若M(x0,y0)是x轴上方抛物线上一点,则(x0﹣a)(x0﹣b)<0;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.其中真命题个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
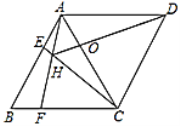
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上的点,且
上的点,且![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论个数是( )
;其中正确的结论个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③![]() .
.
其中正确的是

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
:![]() 的对称轴是
的对称轴是![]() 轴,过点
轴,过点![]() 作一直线与抛物线
作一直线与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 相交于点
相交于点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(3)若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切.过抛物线![]() 上的任意一点(除顶点外)作该抛物线的切线
上的任意一点(除顶点外)作该抛物线的切线![]() ,分别交直线
,分别交直线![]() 和直线
和直线![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 为
为![]() 的直径,过点
的直径,过点![]() 作弦
作弦![]() 垂直于直径
垂直于直径![]() 于
于![]() ,点
,点![]() 恰好为
恰好为![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com