

分析 (1)AB与DF平行.根据翻折可得出∠DFC=∠C,结合∠B=∠C即可得出∠B=∠DFC,从而证出AB∥DF;
(2)连接GC,由翻折可得出∠DGE=∠ACB,再根据三角形外角的性质得出∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,通过角的运算即可得出∠1+∠2=2∠B.
解答 解:(1)AB与DF平行.理由如下:
由翻折,得∠DFC=∠C.
又∵∠B=∠C,
∴∠B=∠DFC,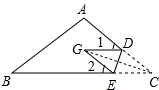
∴AB∥DF.
(2)连接GC,如图所示.
由翻折,得∠DGE=∠ACB.
∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.
点评 本题考查了平行线的判定以及翻折得性质,解题的关键是:(1)找出∠B=∠DFC;(2)根据三角形外角的性质利用角的计算求出∠1+∠2=2∠B.本题属于基础题,难度不大,解决该题型题目时,找出相等(或互补)的角是关键.


科目:初中数学 来源: 题型:填空题
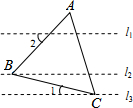 如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.
如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 为抵御百年不遇的洪水,某市政府决定将1200m长的大堤的迎水坡面铺石加固,堤高DF=4m,堤面加宽2m,则完成这一工程需要的石方数为144000m3.
为抵御百年不遇的洪水,某市政府决定将1200m长的大堤的迎水坡面铺石加固,堤高DF=4m,堤面加宽2m,则完成这一工程需要的石方数为144000m3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com