
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD ![]() CD,垂足为D,AD交⊙O 于E,连接CE.
CD,垂足为D,AD交⊙O 于E,连接CE.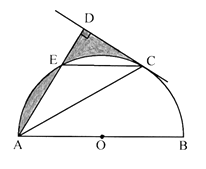
(1)求证:CD 是⊙O 的切线
(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
【答案】
(1)证明:∵AC为∠DAB的平分线,∴∠DAC=∠BAC,∵OA=OC,∴∠OAC=∠OCA,∴∠DAC=∠OCA,∴OC∥AD,∵AD⊥CD,∴OC⊥CD,∴CD与圆O相切;
(2)解:连接EB,交OC于F.
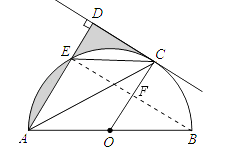
∵E为弧AC的中点,
∴弧AE==弧EC,∴AE=EC,
∴∠EAC=∠ECA.
又∵∠EAC=∠OAC,
∴∠ECA=∠OAC,
∴CE∥OA.
又∵OC∥AD,
∴四边形AOCE是平行四边形,
∴CE=OA,AE=OC.
又∵OA=OC=1,
∴四边形AOCE是菱形.
∵AB为直径,得到∠AEB=90°,
∴EB∥CD.
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF= ![]() AE=
AE= ![]() ,即CF=DE=
,即CF=DE= ![]() ,
,
在Rt△OBF中,根据勾股定理得:EF=FB=DC= ![]() ,则S阴影=S△DEC=
,则S阴影=S△DEC= ![]() .
.
【解析】(1)要证CD与圆O相切,需证OC垂直于CD,结合已知条件,由AC为角平分线得到一对角相等,再由OA=OC,利用等边对等角得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OC与AD平行,根据AD垂直于CD,得到OC垂直于CD,即可得证;
(2)根据E为弧AC的中点,得到弧AE=弧EC,利用等弧对等弦得到AE=EC,可得出弓形AE与弓形EC面积相等,阴影部分面积可转化为为直角三角形DEC的面积,求出S△DEC即可.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 | 芦柑 | 香梨 | |
每辆汽车载货量 | 7 | 6 | 5 |
每车水果获利 | 2500 | 3000 | 2000 |
![]() 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
![]() 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从山脚开始攀登一座600m高的山,第一小组的攀登速度(即攀登高度与攀登时间之比)是第二小组的1.2倍,并比第二小组早20min到达山顶.
(1)第二小组的攀登速度是多少?
(2)如果山高为hm,第一小组的攀登速度是第二小组的k(k>1)倍,并比第二小组早tmin到达山顶,则第一小组的攀登速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() (a是常数,
(a是常数, ![]() ),下列结论正确的是( )
),下列结论正确的是( )
A.当a = 1时,函数图像经过点(一1,0)
B.当a = 一2时,函数图像与x轴没有交点
C.若 ![]() ,函数图像的顶点始终在x轴的下方
,函数图像的顶点始终在x轴的下方
D.若 ![]() ,则当
,则当 ![]() 时,y随x 的增大而增大
时,y随x 的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于结论:当a+b=0时,a3+b3=0也成立.若将a看成a3的立方根,b看成b3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两个数也互为相反数”
(1)举一个具体的例子来判断上述结论是否成立;
(2)若![]() 和
和![]() 互为相反数,且x+5的平方根是它本身,求x+y的立方根.
互为相反数,且x+5的平方根是它本身,求x+y的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a c b ,那么我们规定(a,b)=c,例如:因为23 8 ,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)= ,(4,1)= ,(2,![]() )= ;
)= ;
(2)若记(3,5)=a,(3,6)=b,(3,30)=c,求证: a b c .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习多项式乘以多项式时发现:(![]() x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:![]() x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(![]() x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装店有A、B两种型号的童装,其进价与售价如下表所示:
型号 | 进价(元) | 售价(元) |
A型 | 90 | 108 |
B型 | 100 | 130 |
根据市场需要,服装店决定:购进A种服装的数量要比购进B种服装的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总利润不少于699元.若假设购进B种服装x件,那么:
(1)请写出A、B两种服装全部销售完毕后的总利润y/元用含x/件的式子表示;
(2)请问该服装店有几种满足条件的进货方案?哪种方案获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com