
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,连结
的中点,连结![]() ,将
,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,连结
,连结![]() .若
.若![]() ,
,![]() ,则线段
,则线段![]() 的长为( )
的长为( )
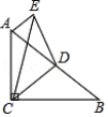
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接BE,延长CD交BE与点H,作CF⊥AB,垂足为F.首先证明DC垂直平分线段BE,△ABE是直角三角形,利用三角形的面积求出EH,得到BE的长,在Rt△ABE中,利用勾股定理即可解决问题.
解:如图,连接BE,延长CD交BE与点H,作CF⊥AB,垂足为F.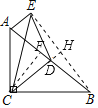
∵在Rt△ABC中,∠ACB=90°,点D是边AB的中点,CD=5,
∴AD=DB=CD=5,AB=10.
∵AC=6,
∴BC=![]() =8.
=8.
∵S△ABC=![]() ACBC=
ACBC=![]() ABCF,
ABCF,
∴![]() ×6×8=
×6×8=![]() ×10×CF,
×10×CF,
解得CF=![]() .
.
∵将△BCD沿直线CD翻折得到△ECD,
∴BC=CE,BD=DE,
∴CH⊥BE,BH=HE.
∵AD=DB=DE,
∴△ABE为直角三角形,∠AEB=90°,
∴S△ECD=S△ACD,
∴![]() DCHE=
DCHE=![]() ADCF,
ADCF,
∵DC=AD,
∴HE=CF=![]() .
.
∴BE=2EH=![]() .
.
∵∠AEB=90°,
∴AE=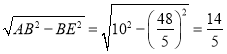 .
.
故选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2+4x+2.
(1)若函数图象与x轴只有一个交点,求m的值;
(2)是否存在整数m,使函数图象与x轴有两个交点,且两交点横坐标差的平方等于8?若存在,求出符合条件的m值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,点M,N在同一个正比例函数图象上的是( )
A.M(2,﹣3),N(﹣4,6)B.M(﹣2,3),N(4,6)
C.M(﹣2,﹣3),N(4,﹣6)D.M(2,3),N(﹣4,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个周末小月和小华在南滨路跑步锻炼身体,两人同时从A点出发,沿直线跑到B点后马上掉头原路返回A点算一个来回,回到A点后又马上调头去往B点,以此类推,每人要完成2个来回。一直两人全程均保持匀速,掉头时间忽略不计。如图所示是小华从出发到他率先完成第一个来回为止,两人到B点的距离之和y(米)与小华跑步时间x(分钟)之间的函数图像,则当小华跑完2个来回时,小月离B点的距离为___米.
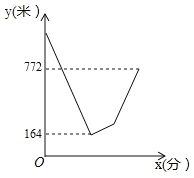
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为□ABCD中一点,EA=ED,∠AED=90,点F,G分别为AB,BC上的点,连接DF,AG,AD=AG=DF,且AG⊥DF于点H,连接EG,DG,延长AB,DG相交于点P.
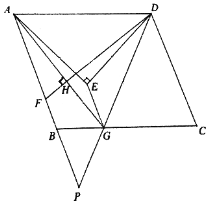
(1)若AH=6,FH=2,求AE的长;
(2)求证:∠P=45;
(3)若DG=2PG,求证:∠AGE=∠EDG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在学习完一次函数与反比例函数的图象与性质后,对函数图象与性质研究饶有兴趣,便想着将一次函数与反比例函数的解析式进行组合研究.他选取特殊的一次函数![]()
![]() 与反比例函数
与反比例函数![]()
![]() ,相加后,得到一个新的函数
,相加后,得到一个新的函数![]()
![]() .已知,这个新函数满足:当
.已知,这个新函数满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求出小林研究的这个组合函数的解析式;
(2)小林依照列表、描点、连线的方法在给定的平面直角坐标系内画出了该函数图象的一部分,请你在图中补全小林未画完的部分,并根据图象,写出该函数图象的一条性质;
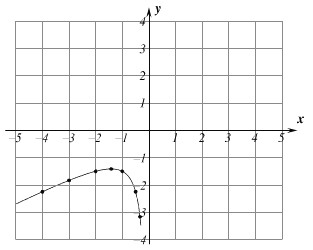
(3)请根据你所画的函数图象,利用所学函数知识,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
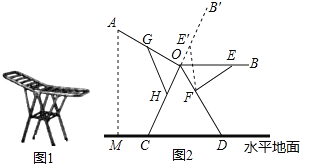
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
(1)求证:直线CD是⊙O的切线;
(2)若CM平分∠ACD,且分别交AD,BD于点M,N,当DM=2时,求MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
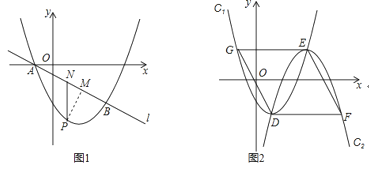
【题目】如图1,抛物线![]() :
:![]() 与直线l:
与直线l:![]() 交于x轴上的一点A,和另一点
交于x轴上的一点A,和另一点![]()
![]() 求抛物线
求抛物线![]() 的解析式;
的解析式;
![]() 点P是抛物线
点P是抛物线![]() 上的一个动点
上的一个动点![]() 点P在A,B两点之间,但不包括A,B两点
点P在A,B两点之间,但不包括A,B两点![]() 于点M,
于点M,![]() 轴交AB于点N,求MN的最大值;
轴交AB于点N,求MN的最大值;
![]() 如图2,将抛物线
如图2,将抛物线![]() 绕顶点旋转
绕顶点旋转![]() 后,再作适当平移得到抛物线
后,再作适当平移得到抛物线![]() ,已知抛物线
,已知抛物线![]() 的顶点E在第一象限的抛物线
的顶点E在第一象限的抛物线![]() 上,且抛持线
上,且抛持线![]() 与抛物线
与抛物线![]() 交于点D,过点D作
交于点D,过点D作![]() 轴交抛物线
轴交抛物线![]() 于点F,过点E作
于点F,过点E作![]() 轴交抛物线
轴交抛物线![]() 于点G,是否存在这样的抛物线
于点G,是否存在这样的抛物线![]() ,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com