
已知点A(a,![]() )、B(2a,y)、C(3a,y)都在抛物线
)、B(2a,y)、C(3a,y)都在抛物线![]() 上.
上.
(1)求抛物线与x轴的交点坐标;
(2)当a=1时,求△ABC的面积;
(3)是否存在含有![]() 、y、y,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
、y、y,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
解:(1)由5![]() =0,······················· (1分)
=0,······················· (1分)
得![]() ,
,![]() .························· (3分)
.························· (3分)
∴抛物线与x轴的交点坐标为(0,0)、(![]() ,0).··········· (5分)
,0).··········· (5分)
(2)当a=1时,得A(1,17)、B(2,44)、C(3,81),········· (6分)
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,则有
![]() =S
=S![]() -
-![]() -
-![]() ················ (7分)
················ (7分)
=![]() -
-![]() -
-![]() ············ (8分)
············ (8分)
=5(个单位面积)······················· (9分)
(3)如:![]() . ······················ (12分)
. ······················ (12分)
事实上,![]() =45a2+36a.
=45a2+36a.
3(![]() )=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.
)=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.
∴![]() .
.


科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
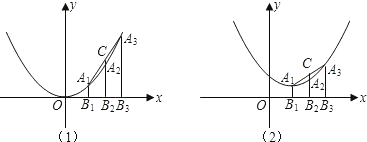 2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com