
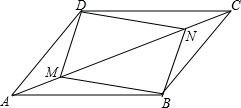
 如图,在?ABCD中,AM=CN,求证:四边形DMBN为平行四边形.
如图,在?ABCD中,AM=CN,求证:四边形DMBN为平行四边形. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
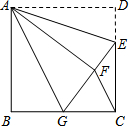 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
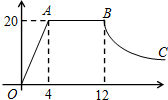 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.如图是某天大棚内温度y(℃)随时间x(小时)变化的函数图象,其中OA段是系统开启后的升温阶段,y与x成正比例,BC段是系统关闭后的降温阶段,y与x成反比例.请根据图中信息解答下列问题:
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.如图是某天大棚内温度y(℃)随时间x(小时)变化的函数图象,其中OA段是系统开启后的升温阶段,y与x成正比例,BC段是系统关闭后的降温阶段,y与x成反比例.请根据图中信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
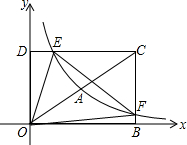 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0),若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0),若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 视力 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
| 人数 | 1 | 2 | 5 | 4 | 3 | 5 | 1 | 2 | 5 | 9 | 6 |
| A. | 5,4 | B. | 4.5,4.5 | C. | 4.9,4.7 | D. | 4.9,4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com